题目内容
抛物线y=-x2上的点到直线4x+3y-8=0距离的最小值是
[ ]
A.![]()
B.![]()
C.![]()
D.3
答案:A
解析:
解析:
|
抛物线y=-x2上到直线4x+3y-8=0的距离最小的点也就是抛物线y=-x2的与4x+3y-8=0平行的切线的切点.于是 ∴x0= 也就是说抛物线y=-x2上的点( |

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
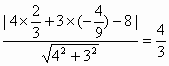 ,故选A.
,故选A.