题目内容
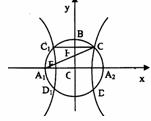
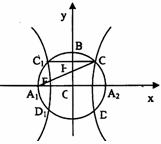
如图,以A1,A2为焦点的双曲线E与半径为c的圆O相交于C,D,C1,D1,连接CC1与OB交于点H,且有: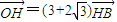 .其中A1,A2,B是圆O与坐标轴的交点,c为双曲线的半焦距.
.其中A1,A2,B是圆O与坐标轴的交点,c为双曲线的半焦距.(1)当c=1时,求双曲线E的方程;
(2)试证:对任意正实数c,双曲线E的离心率为常数.
(3)连接A1C与双曲线E交于F,是否存在
实数λ,使
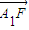 =λ
=λ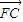 恒成立,若存在,试求出λ的值;若不存在,请说明理由.
恒成立,若存在,试求出λ的值;若不存在,请说明理由.
【答案】分析:(1)根据题意可求得B的坐标和H的坐标,设出曲线E的方程,把点C代入曲线E,利用半焦距c联立方程求得a和b,则曲线E的方程可得.
(2)根据题意可表示出H的坐标,设出曲线E的方程,联立方程求得a和b的关系,进而根据双曲线中a,b和c关系求得a和c的关系,则双曲线的离心率可得.推断出双曲线E的离心率为常数.
(3)先假设存在实数λ,依题意可知C点坐标,利用 =λ
=λ 表示出F的坐标,分别代入双曲线的方程,联立求得λ关于e的表达式,进而根据(2)中e为常数推断出存在实数λ使题设等式成立.
表示出F的坐标,分别代入双曲线的方程,联立求得λ关于e的表达式,进而根据(2)中e为常数推断出存在实数λ使题设等式成立.
解答:解:(1)由c=1知B(0,1),∵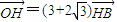 ,
,
∴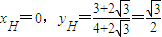
即H(0,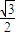 )点C在单位圆上,∴C=(
)点C在单位圆上,∴C=( ,
,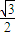 )
)
设双曲线E的方程为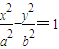 (a>0,b>0).
(a>0,b>0).
由点C的双曲线E上,半焦距c=1有: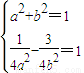
解得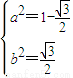
所以双曲线E的方程为: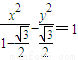
(2)证明:∵A1(-c,0),B(0,c),
由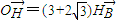 得:H(0,
得:H(0,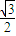 ),(
),( c,
c,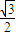 c)
c)
设双曲线E的方程为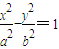 (a>0,b>0)
(a>0,b>0)
∴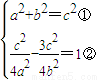
①代入②,化简整理得3a4+6a2b2-b4=0,
∴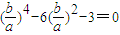
解得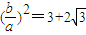
又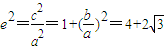 .
.
∴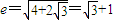 ,即双曲线E的离心离是与c无关的常数.
,即双曲线E的离心离是与c无关的常数.
(3)假设存在实数λ,使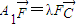 恒成立,
恒成立,
A1(-c,0),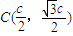 有
有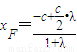 ,
,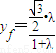
点F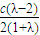 ,
,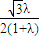 点C,F都在双曲线E上,
点C,F都在双曲线E上,
故有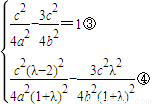
由③得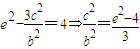 ⑤
⑤
⑤代入④得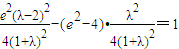 ,
,
化简整理得-λe2+e2=2λ+1
即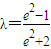 ,利用(2)小题的结论得:
,利用(2)小题的结论得: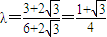
故存在实数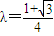 ,使
,使 恒成立.
恒成立.
点评:本题主要考查了直线与圆锥曲线的综合问题,双曲线的标准方程和双曲线的简单性质.考查了运算的能力,分析问题的能力.
(2)根据题意可表示出H的坐标,设出曲线E的方程,联立方程求得a和b的关系,进而根据双曲线中a,b和c关系求得a和c的关系,则双曲线的离心率可得.推断出双曲线E的离心率为常数.
(3)先假设存在实数λ,依题意可知C点坐标,利用
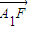 =λ
=λ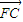 表示出F的坐标,分别代入双曲线的方程,联立求得λ关于e的表达式,进而根据(2)中e为常数推断出存在实数λ使题设等式成立.
表示出F的坐标,分别代入双曲线的方程,联立求得λ关于e的表达式,进而根据(2)中e为常数推断出存在实数λ使题设等式成立.解答:解:(1)由c=1知B(0,1),∵
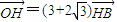 ,
,∴
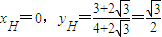
即H(0,
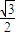 )点C在单位圆上,∴C=(
)点C在单位圆上,∴C=( ,
,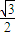 )
)设双曲线E的方程为
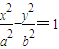 (a>0,b>0).
(a>0,b>0).由点C的双曲线E上,半焦距c=1有:
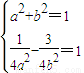
解得
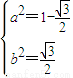
所以双曲线E的方程为:
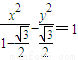
(2)证明:∵A1(-c,0),B(0,c),
由
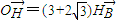 得:H(0,
得:H(0,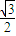 ),(
),( c,
c,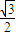 c)
c)设双曲线E的方程为
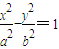 (a>0,b>0)
(a>0,b>0)∴
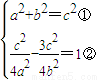
①代入②,化简整理得3a4+6a2b2-b4=0,
∴
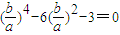
解得
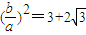
又
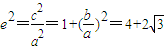 .
.∴
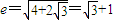 ,即双曲线E的离心离是与c无关的常数.
,即双曲线E的离心离是与c无关的常数.(3)假设存在实数λ,使
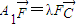 恒成立,
恒成立,A1(-c,0),
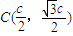 有
有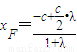 ,
,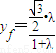
点F
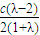 ,
,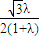 点C,F都在双曲线E上,
点C,F都在双曲线E上,故有
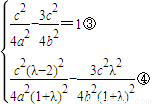
由③得
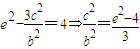 ⑤
⑤⑤代入④得
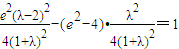 ,
,化简整理得-λe2+e2=2λ+1
即
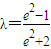 ,利用(2)小题的结论得:
,利用(2)小题的结论得: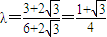
故存在实数
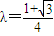 ,使
,使 恒成立.
恒成立.点评:本题主要考查了直线与圆锥曲线的综合问题,双曲线的标准方程和双曲线的简单性质.考查了运算的能力,分析问题的能力.

练习册系列答案
相关题目
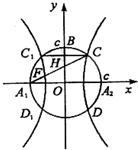 如图,以A1,A2为焦点的双曲线E与半径为c的圆O相交于C,D,C1,D1,连接CC1与OB交于点H,且有:
如图,以A1,A2为焦点的双曲线E与半径为c的圆O相交于C,D,C1,D1,连接CC1与OB交于点H,且有: 随机抽取某产品n件,测得其长度分别为以a1,a2,…,an,则如图所示的程序框图输出的s=
随机抽取某产品n件,测得其长度分别为以a1,a2,…,an,则如图所示的程序框图输出的s=