题目内容
(本小题满分7分)
已知函数
(Ⅰ)当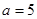 时,求函数
时,求函数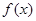 的定义域;
的定义域;
(Ⅱ)当函数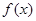 的定义域为R时,求实数
的定义域为R时,求实数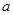 的取值范围。
的取值范围。
【答案】
(1)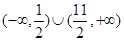 .(2)
.(2)
【解析】
试题分析:解:(Ⅰ)当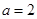 时,要使函数
时,要使函数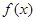 有意义,
有意义,
有不等式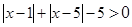 成立,------------------①
成立,------------------①
当 时,不等式①等价于
时,不等式①等价于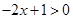 ,即
,即 ,∴
,∴ ;
;
当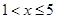 时,不等式①等价于
时,不等式①等价于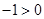 ,∴无解
,∴无解
当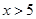 时,不等式①等价于
时,不等式①等价于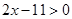 ,即
,即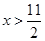 ,∴
,∴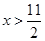 ;
;
综上函数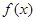 的定义域为
的定义域为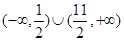 .
.
(Ⅱ)∵函数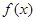 的定义域为
的定义域为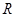 , ∴不等式
, ∴不等式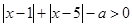 恒成立,
恒成立,
∴只要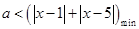 即可,又
即可,又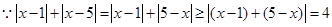
(当且仅当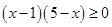 时取等)
时取等)
即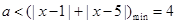 ,∴
,∴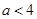 . ∴
. ∴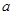 的取值范围是
的取值范围是 .
.
考点:绝对值不等式的求解
点评:解决该试题的关键是利用绝对值的含义以及公式来分情况讨论求解得到,属于基础题。

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 =
= ,变换T的矩阵为A=
,变换T的矩阵为A= ,平面上的点P(1,1)在变换T
,平面上的点P(1,1)在变换T 与圆
与圆 (
( >0)相交于A、B两点,设
>0)相交于A、B两点,设
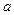 2+
2+ 2恒成立,试求2
2恒成立,试求2 有一个属于特征值1的特征向量
有一个属于特征值1的特征向量 .
. 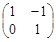 ,点O(0,0),M(2,-1),N(0,2),求
,点O(0,0),M(2,-1),N(0,2),求 在矩阵AB的对应变换作用下所得到的
在矩阵AB的对应变换作用下所得到的 的面积.
的面积.  的参数方程为
的参数方程为 ,曲线
,曲线 的极坐标方程为
的极坐标方程为 .
. ,不等式
,不等式 在
在 上恒成立.
上恒成立. 的取值范围;
的取值范围; ,若正实数
,若正实数 满足
满足 ,求
,求 的最大值.
的最大值.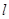 的参数方程为
的参数方程为 (t为参数)。在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为
(t为参数)。在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为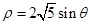 。
。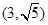 ,求|PA|+|PB|。
,求|PA|+|PB|。