题目内容
平面向量 与
与 夹角为60°,
夹角为60°, ,
, ,则
,则 ( )
( )
A. | B.12 | C.4 | D.2 |
D
解析试题分析:因为, ,所以,
,所以, ,
,
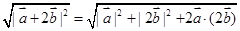 =
=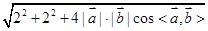 =2
=2 ,
,
故选D。
考点:平面向量的坐标运算,平面向量的数量积。
点评:中档题,涉及平面向量模的计算问题,往往要“化模为方”,转化成平面向量的数量积。

练习册系列答案
相关题目
若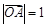 ,
,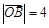 ,
,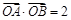 ,
,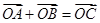 ,则△
,则△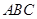 的面积是 ( )
的面积是 ( )
| A.1 | B.2 | C.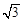 | D.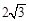 |
已知正三角形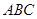 的边长为1,点
的边长为1,点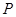 是
是 边上的动点,点
边上的动点,点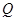 是
是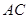 边上的动点,且
边上的动点,且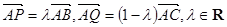 ,则
,则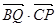 的最大值为
的最大值为
A.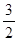 | B.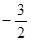 | C.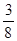 | D.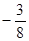 |
已知向量 ,向量
,向量 ,则
,则 的最大值和最小值分别为( )
的最大值和最小值分别为( )
A.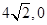 | B.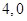 | C. | D. |
已知点 .
. .
. .
.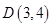 ,则向量
,则向量 在
在 方向上的投影为( )
方向上的投影为( )
A. | B. | C. | D. |
已知 则
则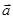 在
在 方向上的投影是( )
方向上的投影是( )
| A.1 | B.-1 | C. | D. |
对任意两个非零的平面向量 和
和 ,定义
,定义 .若平面向量
.若平面向量 ,
, 满足
满足 ,
, 与
与 的夹角
的夹角
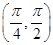 ,且
,且 和
和 都在集合
都在集合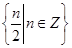 中,则
中,则 =( )
=( )
A. | B. | C.1 | D. |
已知平面上 三点共线,且
三点共线,且 ,则对于函数
,则对于函数 ,下列结论中错误的是( )
,下列结论中错误的是( )
A.周期是 | B.最大值是2 |
C. 是函数的一个对称点 是函数的一个对称点 | D.函数在区间 上单调递增 上单调递增 |
 是坐标原点,两定点
是坐标原点,两定点 满足
满足 ,则点集
,则点集 所表示的区域的面积是( )
所表示的区域的面积是( )


