题目内容
19.(本小题满分8分)已知,过点M(-1,1)的直线l被圆C:x2 + y2-2x + 2y-14 = 0所截得的弦长为4,求直线l的方程.
【答案】
解:由圆的方程可求得圆心C的坐标为(1,-1),半径为4
∵直线l被圆C所截得的弦长为4
∴圆心C到直线l的距离为2
(1)若直线l的斜率不存在,则直线l的方程为x =-1,此时C到l的距离为2,可求得弦长为4,符合题意。
(2)若直线l的斜率存在,设为k, 则直线l的方程为y-1 = k(x + 1)
即kx-y + k + 1 = 0, ∵圆心C到直线l的距离为2
∴ = 2 ∴k2 + 2k + 1 = k2 + 1
∴k = 0 ∴直线l的方程为y =1
综上(1)(2)可得:直线l的方程为x =-1或 y =1.
【解析】略

练习册系列答案
相关题目
 ,满足
,满足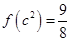
 的值;
的值;
 .
. ,集合A={
,集合A={ ,集合B=
,集合B=
 (2)
(2) 
 ,试确定
,试确定 的值,使得:
的值,使得: ;
(2)
;
(2) 
 ,
,  的夹角为
的夹角为 , 且
, 且 ,
,  ,
,  ; (2) 求
; (2) 求 .
.