题目内容
(1)已知f(x)=2+log4x(1≤x≤16),求函数g(x)=[f(x)]2+f(x2)的值域.
(2)若直线y=4a与y=|ax-2|(a>0且a≠1)的图象有两个公共点,求a的取值范围.
(2)若直线y=4a与y=|ax-2|(a>0且a≠1)的图象有两个公共点,求a的取值范围.
分析:(1)先求出函数y=[f(x)]2+f(x2)的定义域,然后将函数化成关于log4x的二次函数,进行配方找出对称轴,而0≤log4x≤2,利用对称轴与区间的位置关系求出最值,即可求出值域.
(2)分别作出直线y=4a与y=|ax-2|(a>0且a≠1)的图象,如图所示,由数形结合易得结果.
(2)分别作出直线y=4a与y=|ax-2|(a>0且a≠1)的图象,如图所示,由数形结合易得结果.
解答: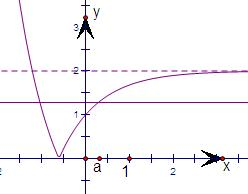 解:(1)由已知得:
解:(1)由已知得:
又
⇒1≤x≤4,
令log4x=t,则g(x)=h(t)=t2+6t+6(0≤t≤1)
∵h(t)在[0,1]上为增函数,
∴h(t)min=h(0)=6,h(t)max=h(1)=13,
∴g(x)的值域为[6,13].
(2)直线y=4a与y=|ax-2|(a>0且a≠1)的图象,如图所示,
直线y=4a与y=|ax-2|(a>0且a≠1)的图象有两个公共点,
由数形结合易得:0<a<
.
 解:(1)由已知得:
解:(1)由已知得:
|
又
|
令log4x=t,则g(x)=h(t)=t2+6t+6(0≤t≤1)
∵h(t)在[0,1]上为增函数,
∴h(t)min=h(0)=6,h(t)max=h(1)=13,
∴g(x)的值域为[6,13].
(2)直线y=4a与y=|ax-2|(a>0且a≠1)的图象,如图所示,
直线y=4a与y=|ax-2|(a>0且a≠1)的图象有两个公共点,
由数形结合易得:0<a<
| 1 |
| 2 |
点评:主要考查了带绝对值的函数、函数的值域.本题以对数函数为载体考查二次函数的值域,属于求二次函数的最值问题,解题的关键是定义域,属于基本题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知f(x)的定义域为x∈R且x≠1,已知f(x+1)为奇函数,当x<1时,f(x)=2x2-x+1,那么,当x>1时,f(x)的递减区间是( )
A、[
| ||
B、[1,
| ||
C、[
| ||
D、(1,
|