题目内容
(19)如图,在长方体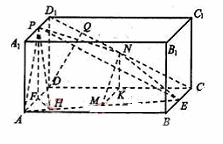
(Ⅰ)求证:![]() 面
面![]() ;
;
(Ⅱ)求二面角![]() 的大小。
的大小。
(Ⅲ)求三棱锥![]() 的体积。
的体积。
本小题主要考察长方体的概念、直线和平面、平面和平面的关系等基础知识,以及空间想象能力和推理能力。
解法一:(Ⅰ)证明:取![]() 的中点
的中点![]() ,连结
,连结![]()
∵![]() 分别为
分别为![]() 的中点
的中点
∵![]()
∴![]() 面
面![]() ,
,![]() 面
面![]()
∴面![]() 面
面![]() ∴
∴![]() 面
面![]()

(Ⅱ)设![]() 为
为![]() 的中点
的中点
∵![]() 为
为![]() 的中点 ∴
的中点 ∴![]() ∴
∴![]() 面
面![]()
作![]() ,交
,交![]() 于
于![]() ,连结
,连结![]() ,则由三垂线定理得
,则由三垂线定理得![]()
从而![]() 为二面角
为二面角![]() 的平面角。
的平面角。
在![]() 中,
中,![]() ,
,
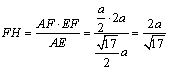
在![]() 中,
中,![]()
故:二面角![]() 的大小为
的大小为![]()
(Ⅲ)![]()
作![]() ,交
,交![]() 于
于![]() ,由
,由![]() 面
面![]() 得
得![]()
∴![]() 面
面![]()
∴在![]() 中,
中,![]()
∴![]()
![]()
![]()
解法二:以![]() 为原点,
为原点,![]() 所在的直线分别为
所在的直线分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴,建立直角坐标系,则
轴,建立直角坐标系,则
![]()
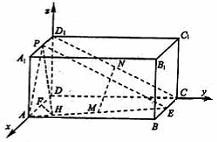
∵![]() 分别是
分别是![]() 的中点
的中点
∴![]()
(Ⅰ)![]()
取n=(0,1,0),显然n![]() 面
面![]()
![]() ·n=0,∴
·n=0,∴![]()
![]() n
n
又![]() 面
面![]() ∴
∴![]() 面
面![]()
(Ⅱ)过![]() 作
作![]() ,交
,交![]() 于
于![]() ,取
,取![]() 的中点
的中点![]() ,则
,则![]()
设![]() ,则
,则![]()
又![]()
由![]() ,及
,及![]() 在直线
在直线![]() 上,可得:
上,可得: 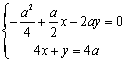
解得![]()
∴![]() ∴
∴![]() 即
即![]()
∴![]() 与
与![]() 所夹的角等于二面角
所夹的角等于二面角![]() 的大小
的大小
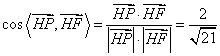
故:二面角![]() 的大小为
的大小为![]()
(Ⅲ)设n1=(x1,y1,z1)为平面![]() 的法向量,则n1
的法向量,则n1![]()
![]() , n1
, n1![]()
![]()
又![]()
∴ 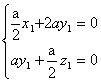
即 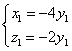
∴可取n1=(4,-1,2)
∴![]() 点到平面
点到平面![]() 的距离为
的距离为
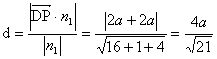
∵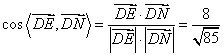 ,
, ![]()
∴![]()
∴![]()

练习册系列答案
相关题目
 如图,在长方体中,
如图,在长方体中,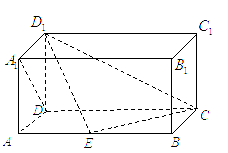 如图,在长方体
如图,在长方体 中,
中, ,
, 则
则 与平面
与平面 所成角的正弦值为 ( )
所成角的正弦值为 ( )
 B.
B. C.
C. D.
D.
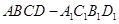 中,已知上下两底面为正方形,且边长均为1;侧棱
中,已知上下两底面为正方形,且边长均为1;侧棱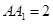 ,
,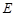 为
为 中点,
中点,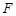 为
为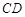 中点,
中点, 为
为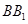 上一个动点.
上一个动点.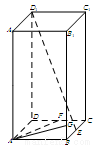
 ;
;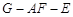 的平面角余弦值.
的平面角余弦值.