题目内容
已知 是椭圆的两个焦点,过
是椭圆的两个焦点,过 的直线
的直线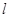 交椭圆于
交椭圆于 两点,若
两点,若 的周长为
的周长为 ,则椭圆方程为( )
,则椭圆方程为( )
 是椭圆的两个焦点,过
是椭圆的两个焦点,过 的直线
的直线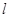 交椭圆于
交椭圆于 两点,若
两点,若 的周长为
的周长为 ,则椭圆方程为( )
,则椭圆方程为( )A. | B. |
C.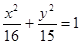 | D.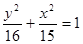 |
A
试题分析:∵
 是椭圆的两个焦点∴c=1,又根据椭圆的定义,
是椭圆的两个焦点∴c=1,又根据椭圆的定义, 的周长=4a=8,得a=2,进而得b=
的周长=4a=8,得a=2,进而得b= ,所以椭圆方程为
,所以椭圆方程为 .
.
练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
题目内容
 是椭圆的两个焦点,过
是椭圆的两个焦点,过 的直线
的直线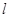 交椭圆于
交椭圆于 两点,若
两点,若 的周长为
的周长为 ,则椭圆方程为( )
,则椭圆方程为( )A. | B. |
C.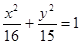 | D.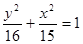 |
 是椭圆的两个焦点∴c=1,又根据椭圆的定义,
是椭圆的两个焦点∴c=1,又根据椭圆的定义, 的周长=4a=8,得a=2,进而得b=
的周长=4a=8,得a=2,进而得b= ,所以椭圆方程为
,所以椭圆方程为 .
.
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案