题目内容
设关于x的方程2x2+ax-9=0,bx2+x-6=0的解集分别为A、B,且A∩B={
}.
(Ⅰ) 求a和b的值;
(Ⅱ) 求函数f(x)=ax2+bx-8的零点.
| 3 | 2 |
(Ⅰ) 求a和b的值;
(Ⅱ) 求函数f(x)=ax2+bx-8的零点.
分析:( I)由题意可得两方程都有一根为x=
,代入可得答案;( II)由( I)的结果可得函数的解析式,分解因式易得零点.
| 3 |
| 2 |
解答:解:( I)由题意可得两方程都有一根为x=
,
代入可得2(
)2+
x-9=0,,b(
)2+
-6=0,
解得:a=3,b=2 (6分)
( II)由( I)可知a=3,b=2,
故f(x)=3x2+2x-8=(x+2)(3x-4)
故函数的零点为:x1=
,x2=-2(6分)
| 3 |
| 2 |
代入可得2(
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
解得:a=3,b=2 (6分)
( II)由( I)可知a=3,b=2,
故f(x)=3x2+2x-8=(x+2)(3x-4)
故函数的零点为:x1=
| 4 |
| 3 |
点评:本题考查函数的零点,涉及方程的根与集合,属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
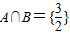 .
.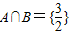 .
.