题目内容
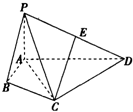 (2012•河南模拟)如图,在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,AB=1,PA=2.
(2012•河南模拟)如图,在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,AB=1,PA=2.(I)证明:直线CE∥平面PAB;
(Ⅱ)求直线CE与平面PAC所成角的余弦值.
分析:(I)取AD中点M,利用三角形的中位线证明EM∥平面PAB,利用同位角相等证明MC∥AB,得到平面EMC∥平面PAB,证得EC∥平面PAB;
(Ⅱ)证明平面DPC⊥平面PAC,作EH⊥PC于H,则EH⊥平面PAC,所以∠ECH为直线CE与平面PAC所成角,计算CE,EH,即可求得结论.
(Ⅱ)证明平面DPC⊥平面PAC,作EH⊥PC于H,则EH⊥平面PAC,所以∠ECH为直线CE与平面PAC所成角,计算CE,EH,即可求得结论.
解答: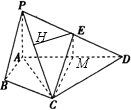 (I)证明:取AD中点M,连EM,CM,则EM∥PA.
(I)证明:取AD中点M,连EM,CM,则EM∥PA.
∵EM?平面PAB,PA?平面PAB,
∴EM∥平面PAB.
在Rt△ACD中,∠CAD=60°,AC=AM=2,∴∠ACM=60°.
而∠BAC=60°,∴MC∥AB.
∵MC?平面PAB,AB?平面PAB,∴MC∥平面PAB.
∵EM∩MC=M,∴平面EMC∥平面PAB.
∵EC?平面EMC,∴EC∥平面PAB.
(Ⅱ)解:∵PA⊥平面ABCD,CD?平面ABCD,∴PA⊥CD
∵∠ACD=90°,PA∩AC=A
∴CD⊥平面PAC
∵CD?平面DPC
∴平面DPC⊥平面PAC
作EH⊥PC于H,则EH⊥平面PAC
∴∠ECH为直线CE与平面PAC所成角
在直角△PCD中,CD=2
,PC=2
,∴PD=2
∵E为中点,EH∥CD
∴CE=
,EH=
∴sin∠ECH=
=
∴cos∠ECH=
∴直线CE与平面PAC所成角的余弦值为
.
 (I)证明:取AD中点M,连EM,CM,则EM∥PA.
(I)证明:取AD中点M,连EM,CM,则EM∥PA.∵EM?平面PAB,PA?平面PAB,
∴EM∥平面PAB.
在Rt△ACD中,∠CAD=60°,AC=AM=2,∴∠ACM=60°.
而∠BAC=60°,∴MC∥AB.
∵MC?平面PAB,AB?平面PAB,∴MC∥平面PAB.
∵EM∩MC=M,∴平面EMC∥平面PAB.
∵EC?平面EMC,∴EC∥平面PAB.
(Ⅱ)解:∵PA⊥平面ABCD,CD?平面ABCD,∴PA⊥CD
∵∠ACD=90°,PA∩AC=A
∴CD⊥平面PAC
∵CD?平面DPC
∴平面DPC⊥平面PAC
作EH⊥PC于H,则EH⊥平面PAC
∴∠ECH为直线CE与平面PAC所成角
在直角△PCD中,CD=2
| 3 |
| 2 |
| 5 |
∵E为中点,EH∥CD
∴CE=
| 5 |
| 3 |
∴sin∠ECH=
| EH |
| EC |
| ||
| 5 |
∴cos∠ECH=
| ||
| 5 |
∴直线CE与平面PAC所成角的余弦值为
| ||
| 5 |
点评:本题考查线面平行,考查线面角,解题的关键是掌握线面平行的判定定理,正确作出线面角,属于中档题.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
 (2012•河南模拟)如图,在四棱锥P-ABCD中,侧棱PA⊥底面ABCD,底面ABCD为矩形,AD=2AB=2PA,E为PD的上一点,且PE=2ED,F为PC的中点.
(2012•河南模拟)如图,在四棱锥P-ABCD中,侧棱PA⊥底面ABCD,底面ABCD为矩形,AD=2AB=2PA,E为PD的上一点,且PE=2ED,F为PC的中点.