题目内容
(本题满分12分)
质点A位于数轴x=0处,质点B位于x=2处.这两个质点每隔1秒钟都向左或
向右平移一个单位,设向左移动的概率为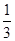 ,向右移动的概率为
,向右移动的概率为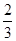 .
.
(I)求3秒后,质点A在点x=1处的概率;
(II)求2秒后,质点A、B同时在x=2处的概率.
【答案】
(1) P1=P3(1)=C31·p(1-p)2=3×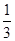 ×(
×(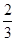 )2=
)2=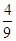 ;
;
(2) P2=P2(0)·P2(1)=C20·(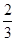 )2·C21·
)2·C21·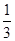 ·
·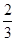 =
=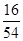 。
。
【解析】(1)本题是一个独立重复试验,向右移动的概率为
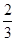 ,向左移的概率为
,向左移的概率为
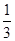 ,根据独立重复试验的概率公式写出第三秒时,粒子A在点x=1处的概率.
,根据独立重复试验的概率公式写出第三秒时,粒子A在点x=1处的概率.
(2)粒子A,B同在点x=2处表示A在这个位置,B也在这个位置,这两个事件是相互独立的,根据相互独立事件同时发生的概率,得到两个粒子同时在规定位置的概率.
(1)质点n次移动看作n次独立重复试验,记向左移动一次为事件A,
则P(A)= 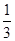 ,P(
,P(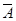 )=
)=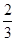 3秒后,质点A在点x=1处的概率P1=P3(1)=C31·p(1-p)2=3×
3秒后,质点A在点x=1处的概率P1=P3(1)=C31·p(1-p)2=3×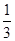 ×(
×(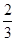 )2=
)2=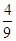 (6’)
(6’)
(2)2秒后,质点A、B同在x=2处,即A、B两质点各做二次移动,其中质点A向右移动2次,质点B向左、向右各移动一次,故P2=P2(0)·P2(1)=C20·(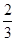 )2·C21·
)2·C21·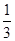 ·
·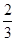 =
=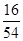 (12’)
(12’)

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
 <1,xÎR }.
<1,xÎR }. ,求实数a的取值范围.
,求实数a的取值范围. (
( ,
, 为常数),且方程
为常数),且方程 有两个实根为
有两个实根为 .
. 的解析式;
的解析式; 中,四边形
中,四边形 是边长为
是边长为 的正方形,
的正方形, ,
, 为
为 上的点,且
上的点,且 ⊥平面
⊥平面
 ⊥平面
⊥平面
 的大小;
的大小; 到平面
到平面