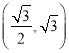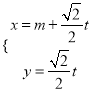题目内容
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,离心率为
,离心率为![]() ,点
,点![]() 是椭圆上任意一点,
是椭圆上任意一点, ![]() 的周长为
的周长为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
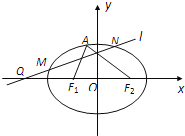
(Ⅱ)过点![]() (-4,0)任作一动直线
(-4,0)任作一动直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,记
两点,记![]() ,若在线段
,若在线段![]() 上取一点
上取一点![]() ,使得
,使得![]() ,则当直线
,则当直线![]() 转动时,点
转动时,点![]() 在某一定直线上运动,求该定直线的方程.
在某一定直线上运动,求该定直线的方程.
【答案】(Ⅰ) ![]() ;(Ⅱ) 点
;(Ⅱ) 点![]() 在定直线
在定直线![]() 上.
上.
【解析】试题分析: (1)由已知条件求出![]() 的值, 根据
的值, 根据![]() ,求出椭圆的方程; (2)设直线
,求出椭圆的方程; (2)设直线![]() 联立直线与椭圆方程, 求出
联立直线与椭圆方程, 求出![]() 的表达式,将
的表达式,将![]() 由
由![]() 表示出来,由
表示出来,由![]() ,求出
,求出![]() 的表达式,化简,求出为定值.
的表达式,化简,求出为定值.
试题解析: (Ⅰ)因为![]() 的周长为
的周长为![]() ,
,
所以![]() ,即
,即![]() .
.
又离心率![]() ,解得
,解得![]() ,
,
![]() .
.
所以椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)由题意可知,直线![]() 的斜率必存在.
的斜率必存在.
故可设直线![]() 的方程为
的方程为![]() ,
,
由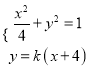 ,消去
,消去![]() 得
得![]() ,
,
由根与系数的关系得![]() ,
,
由![]() ,得
,得![]()
所以![]() .
.
所以![]() ,
,
设点![]() 的坐标为
的坐标为![]() ,
,
由![]() ,得
,得![]() ,
,
所以![]() ,
,
解得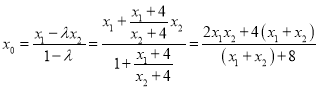 .
.
而![]() ,
,
![]() ,
,
所以![]() .
.
故点![]() 在定直线
在定直线![]() 上.
上.
点睛: 本题主要考查了以椭圆为载体,求椭圆标准方程以及椭圆与直线的关系 ,属于中档题. 考点有: 椭圆的标准方程,椭圆的简单几何性质,韦达定理,向量坐标运算等等. 考查学生的逻辑思维能力,运算求解能力.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案【题目】某社区超市购进了A,B,C,D四种新产品,为了解新产品的销售情况,该超市随机调查了15位顾客(记为![]() )购买这四种新产品的情况,记录如下(单位:件):
)购买这四种新产品的情况,记录如下(单位:件):
顾 客 产 品 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A | 1 | 1 | 1 | 1 | 1 | ||||||||||
B | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |||||||
C | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||||||
D | 1 | 1 | 1 | 1 | 1 | 1 |
(Ⅰ)若该超市每天的客流量约为300人次,一个月按30天计算,试估计产品A的月销售量(单位:件);
(Ⅱ)为推广新产品,超市向购买两种以上(含两种)新产品的顾客赠送2元电子红包.现有甲、乙、丙三人在该超市购物,记他们获得的电子红包的总金额为X,
求随机变量X的分布列和数学期望;
(Ⅲ)若某顾客已选中产品B,为提高超市销售业绩,应该向其推荐哪种新产品?(结果不需要证明)