题目内容
已知 ,
, 等差中项是
等差中项是 ,且
,且 ,
,  ,则
,则 最小值( )
最小值( )
| A.3 | B.4 | C.5 | D.6 |
C
解析试题分析:因为 ,且
,且 等差中项是
等差中项是 ,有a+b=1,那么则
,有a+b=1,那么则 ,结合均值不等式的性质可知,
,结合均值不等式的性质可知, 取得等号,故
取得等号,故 ,选C.
,选C.
考点:本题主要考查均值不等式求解最值的运用。
点评:解决该试题的关键是能整体利用合理的组合,结合均值不等式的思想,一正二定三相等的思想来求解最值。

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
若 ,且
,且 .则
.则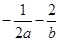 的最大值是( )
的最大值是( )
A.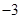 | B. | C.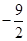 | D. |
若对于使 成立的所有常数
成立的所有常数 中,我们把
中,我们把 的最小值
的最小值 叫做
叫做 的上确界,若
的上确界,若 ,则
,则 的上确界是( )
的上确界是( )
A. | B.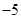 | C. | D.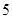 |
对一切实数x,不等式 恒成立,则实数a的取值范围是( )
恒成立,则实数a的取值范围是( )
A.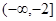 | B. | C. | D. |
若三点 (2,2),
(2,2),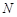 (
( ,0),
,0), (0,
(0,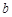 ),(
),( )共线,则
)共线,则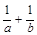 的值为( )
的值为( )
| A.1 | B. | C. | D. |
函数 在区间
在区间 上的最小值是( )
上的最小值是( )
A. | B. | C. | D. |
若 ,则
,则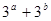 的最小值( )
的最小值( )
| A.4 | B.5 | C.6 | D.7 |
已知 ,则函数
,则函数 的最小值为
的最小值为
| A.1 | B.2 | C.3 | D.4 |
 ,过定点A的动直线
,过定点A的动直线 和过定点B的动直线
和过定点B的动直线 交于点
交于点 ,则
,则 的最大值是 .
的最大值是 .