题目内容
()设![]() ,
,![]() 为常数).当
为常数).当![]() 时,
时,![]() ,且
,且![]() 为
为![]() 上的奇函数.
上的奇函数.
⑴ 若![]() ,且
,且![]() 的最小值为
的最小值为![]() ,求
,求![]() 的表达式;
的表达式;
⑵ 在 ⑴ 的条件下,![]() 在
在![]() 上是单调函数,求
上是单调函数,求![]() 的取值范围.
的取值范围.
(1)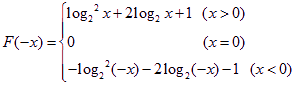
(2)![]() 或
或![]()
解析:
(1) ![]() 由
由![]() 得
得![]() ,
,
∴![]()
若![]() 则
则![]() 无最小值. ∴
无最小值. ∴![]() .
.
欲使![]() 取最小值为0,只能使
取最小值为0,只能使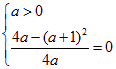 ,解得
,解得![]() ,
,![]() .
.
∴![]()
得![]() 则
则![]() ,∴
,∴![]()
又![]() ,∴
,∴![]()
又![]() ∴
∴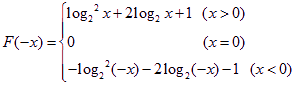
(2)![]()
![]() ,
,![]() .
.
得![]() ,则
,则![]() ,
,![]() .
.
∴当![]() ,或
,或![]() 或
或![]() 时,
时,![]() 为单调函数.
为单调函数.
综上,![]() 或
或![]() .
.

练习册系列答案
相关题目