题目内容

设b为常数，f（x）=|x2-1|+x2+bx（x∈R）
（1）当b=2时，求方程f（x）=0的解；
（2）若关于x的方程f（x）=0在（0，2）上有两个解x1，x2，证明：
1
x1
+
1
x2
＜4．
分析：（1）b=2时，方程f（x）=0即：|x2-1|+x2+2x=0，分类讨论：当x2-1≥0时，x2-1+x2+2x=0，当x2-1＜0时，-x2+1+x2+2x=0，分别解出方程的根，从而得出方程f（x）=0的解；
（2）若关于x的方程f（x）=0在（0，2）上有两个解x1，x2，不妨设x1＜x2，如图，结合图形得到b的取值范围，将
1
x1
+
1
x2
表示成b的函数，再利用函数的单调性即可证得．
解答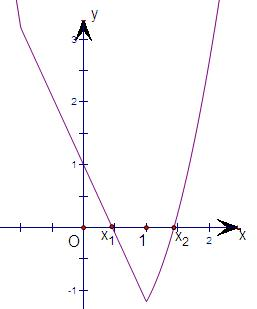：解：（1）b=2时，方程f（x）=0即：
|x2-1|+x2+2x=0，
当x2-1≥0时，x2-1+x2+2x=0，解得：x=
-1-
3
2
；
当x2-1＜0时，-x2+1+x2+2x=0，解得：x=-
1
2
；
∴方程f（x）=0的解为：x=
-1-
3
2
；或x=-
1
2
；
（2）若关于x的方程f（x）=0在（0，2）上有两个解x1，x2，
不妨设x1＜x2，如图，
类似于（1）得：x1=-
1
b
，x2=
-b+
b 2+8
4
，
且-
7
2
＜b＜-1．
则
1
x1
+
1
x2
=-b+
4
-b+
b 2+8
=-b+
b+
b 2+8
2
=
-b+
b 2+8
2
，
它在区间（-
7
2
，-1）上是减函数，
∴
-b+
b 2+8
2
＜
7
2
+
(-
7
2
)2+8
2
=4，
∴
1
x1
+
1
x2
＜4．
点评：本小题主要考查函数单调性的应用、根与系数的关系、带绝对值的函数等基础知识，考查运算求解能力，考查数形结合思想、化归与转化思想．属于中档题．
练习册系列答案
相关题目
设f(x)=alog22x+blog4x2+1，（a，b为常数）．当x＞0时，F（x）=f（x），且F（x）为R上的奇函数．
（Ⅰ）若f(
1
2
)=0，且f（x）的最小值为0，求F（x）的表达式；
（Ⅱ）在（Ⅰ）的条件下，g(x)=
f(x)+k-1
log2x
在[2，4]上是单调函数，求k的取值范围．
已知定理：“若a，b为常数，g（x）满足g（a+x）+g（a-x）=2b，则函数y=g（x）的图象关于点（a，b）中心对称”．设函数f(x)=
x+1-a
a-x
，定义域为A．
（1）试证明y=f（x）的图象关于点（a，-1）成中心对称；
（2）当x∈[a-2，a-1]时，求证：f(x)∈[-
1
2
， 0]；
（3）对于给定的x1∈A，设计构造过程：x2=f（x1），x3=f（x2），…，xn+1=f（xn）．如果xi∈A（i=2，3，4…），构造过程将继续下去；如果xi∉A，构造过程将停止．若对任意x1∈A，构造过程都可以无限进行下去，求a的值．
设函数f（x）=ax+b，其中a，b为常数，f1（x）=f（x），fn+1（x）=f（fn（x）），n∈N*，若f3（x）=8x+21，则ab=
6
6
，fn（x）=
2nx+3×2n-3
2nx+3×2n-3
．
已知定理：“若a，b为常数，g（x）满足g（a+x）+g（a-x）=2b．则函数y=g（x）的图象关于点（a，b）成中心对称”．设函数f（x）=
x+1-aa-x
，定义域为A．
（1）试证明y=f（x）的图象关于点（a，-1）成中心对称；
（2）写出f（x）的单调区间（不证明），并求当x∈[a-2，a-1]时，函数f（x）的值域；
（3）对于给定的x1∈A，设计构造过程：x2=f（x1），x3=f（x2），…，xn+1=f（xn）．如果xi∈A（i=1，2，3，4…），构造过程将继续下去；如果xi∉A，构造过程将停止．若对任意x1∈A，构造过程都可以无限进行下去，求a的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网