Question

A、B、C是半径为1的球面上三点,B、C两点间的球面距离为,点A与B、C两点间的球面距离为,球心为O,求:

(1)∠BOC、∠AOB的大小;

(2)球心到截面ABC的距离.

Answer 1

解析:(1)∠BOC=,∠AOB=.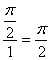

 (2)连结OA、OB、OC、AB、AC、BC得三棱锥O—ABC,设OH⊥平面ABC于H,则h=OH为球心到截面ABC的距离.由OA⊥OB,OA⊥OC得OA⊥平面OBC,V_O—ABC=·1·S_△OBC=×.

又V_O—ABC=·h·S_△ABC=·h··,

∴=h,即h=.