题目内容

下列函数中，最小值为4的有多少个？
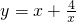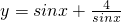① $数学公式$ 　　 ② $数学公式$ （0＜x＜π）　　 ③y=e^x+4e^-x④y=log₃x+4log_x3．

A.
4
B.
3
C.
2
D.
1

D
分析：对于①，取特殊值x=-1时，y=-5显然最小值不是4，对于②最小值取4时sinx=2，这不可能；对于③可以直接利用基本不等式求解即可；对于④根据基本不等式成立的条件满足时，运用基本不等式即可求出最小值．
解答：①y=x+ $\text{[math]}$ ，当x=-1时，y=-5显然最小值不是4，故不正确；
②y=sinx+ $\text{[math]}$ （0＜x＜π），y=sinx+ $\text{[math]}$ ≥4，此时sinx=2，这不可能，故不正确；
③y=e^x+4e^-x≥4，当且仅当x=ln2时等号成立．
④y=log₃x+4log_x3，当log₃x＞0，log_x3＞0，∴y=log₃x+4log_x3≥4，此时x=9，当log₃x＜0，log_x3＜0故不正确；
故选D．
点评：本题主要考查了利用基本不等式求函数的值域，解题的关键是最值能否取到，属于中档题．