题目内容
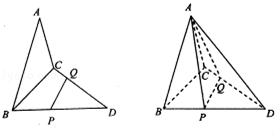
如图1,直角梯形 中,
中, ,
,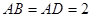 ,
,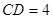 ,点
,点 为线段
为线段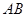 上异于
上异于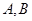 的点,且
的点,且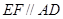 ,沿
,沿 将面
将面 折起,使平面
折起,使平面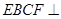 平面
平面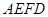 ,如图2.
,如图2.
(1)求证: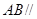 平面
平面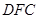 ;
;
(2)当三棱锥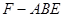 体积最大时,求平面
体积最大时,求平面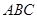 与平面
与平面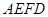 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.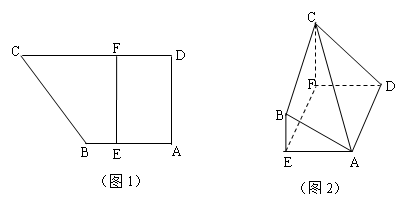
(1)证明过程详见解析;(2) .
.
解析试题分析:本题考查立体几何中的线面、面面关系,空间角,空间向量在立体几何中的应用等基础知识;考查运算求解能力、空间想象能力;考查数形结合思想、化归与转化等数学思想.第一问,法一,由 ,利用线面平行的判定得
,利用线面平行的判定得 面
面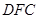 ,再利用面面平行的判定得面
,再利用面面平行的判定得面 面
面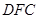 ,最后利用面面平行的性质得
,最后利用面面平行的性质得 面
面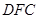 ;法二,建立空间直角坐标系,要证明线面平行,只需证AB与面DFC的法向量垂直即可;第二问,建立空间直角坐标系,利用三棱锥的体积公式计算体积,当体积最大值时,AE=1,再利用向量法求平面ABC和平面AEFD的法向量,利用夹角公式求二面角的余弦值.
;法二,建立空间直角坐标系,要证明线面平行,只需证AB与面DFC的法向量垂直即可;第二问,建立空间直角坐标系,利用三棱锥的体积公式计算体积,当体积最大值时,AE=1,再利用向量法求平面ABC和平面AEFD的法向量,利用夹角公式求二面角的余弦值.
试题解析:(1)证明:∵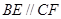 ,
,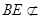 面
面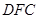 ,
,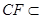 面
面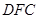 ,
,
∴ 面
面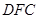 , 2分
, 2分
同理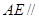 面
面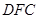 , 3分
, 3分
又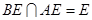 ,∴面
,∴面 面
面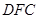 , 4分
, 4分
又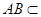 面
面 ,∴
,∴ 面
面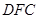 . 5分
. 5分
(2)法一:∵面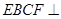 面
面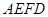 ,又
,又 ,面
,面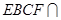 面
面 ,
,
∴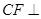 面
面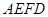 .
.
以 所在直线为
所在直线为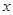 轴,
轴,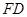 所在直线为
所在直线为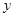 轴,
轴, 所在直线为
所在直线为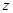 轴,建立
轴,建立
空间直角坐标系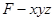 , 7分
, 7分
设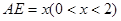 ,则
,则 ,
,
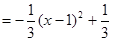 ,
,
∴当 时,三棱锥
时,三棱锥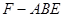 体积最大. 9分
体积最大. 9分
∵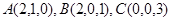 , ∴
, ∴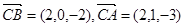 , 10分
, 10分
设平面 的法向量
的法向量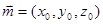 ,
,  , ∴
, ∴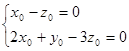 ,
,
令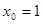 ,得平面
,得平面

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
 中,
中,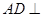 平面
平面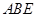 ,
,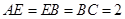 ,
, 为
为 上的点,
上的点, 平面
平面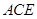
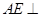 平面
平面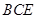 ;
;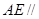 平面
平面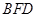 ;
;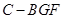 的体积。
的体积。

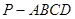 的底面为菱形,
的底面为菱形,
 面
面 ,且
,且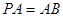 ,
,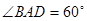 ,
,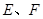 分别是
分别是 的中点.
的中点.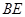 ∥平面
∥平面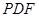 ;
;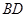 作一平面交棱
作一平面交棱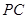 于点
于点 ,若二面角
,若二面角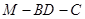 的大小为
的大小为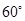 ,求
,求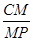 的值.
的值.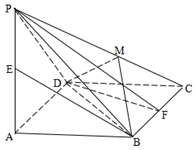

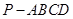 中,
中, ,底面
,底面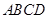 为梯形,
为梯形,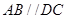 ,
, ,且
,且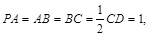
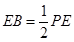 .(10分)
.(10分)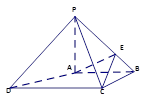
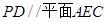 ;
;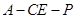 的余弦值.
的余弦值.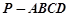 的底面
的底面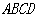 是平行四边形,
是平行四边形,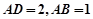 ,
,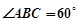 ,
, 面
面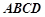 ,设
,设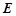 为
为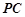 中点,点
中点,点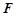 在线段
在线段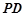 上且
上且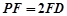 .
.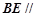 平面
平面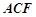 ;
;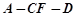 的大小为
的大小为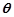 ,若
,若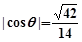 ,求
,求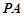 的长.
的长.
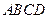 的顶点
的顶点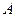 ,
,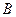 ,
,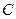 分别在两两垂直的三条射线
分别在两两垂直的三条射线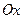 ,
,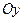 ,
,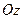 上,则在下列命题中,正确命题的个数为_______.
上,则在下列命题中,正确命题的个数为_______.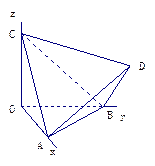
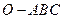 是正三棱锥 ;
是正三棱锥 ;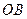 ∥平面
∥平面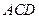 ;
;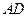 与
与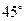 ;
;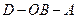 为
为