题目内容
函数f(x)=ax2+3ax+1,若f(x)>f′(x)对一切x∈R恒成立,则实数a的取值范围是( )A.a<
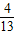
B.a≥0
C.0<a<
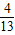
D.0≤a<
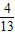
【答案】分析:本题先求出函数f(x)的导数,利用f(x)>f′(x)化简得到含参数a的二次不等式ax2+ax+1-3a>0对一切x∈R恒成立,构造函数得到形式上的二次函数g(x)=ax2+ax+1-3a后,对于g(x)>0恒成立问题,要注意对参数a分类讨论,容易地得出解答.
解答:解:因为f′(x)=2ax+3a,所以由f(x)>f′(x)得ax2+3ax+1>2ax+3a,即有:ax2+ax+1-3a>0对一切x∈R恒成立,
设g(x)=ax2+ax+1-3a,
①当a=0时,g(x)=1>0恒成立,
②当a≠0时,若使g(x)=ax2+ax+1-3a>0恒成立,由g(x)=的对称轴x=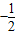 ,则有:
,则有:
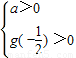 ,即
,即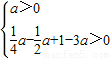 ,得
,得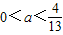 ,
,
综合①②得实数a的取值范围是: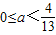
故应选:D
点评:本题考查一元二次不等式的应用,含参不等式的恒成立问题的求解,综合考查了利用函数的倒数来解决问题的能力,分类讨论和转化与化归思想的应用;对运算能力,思维能力亦有所要求.
解答:解:因为f′(x)=2ax+3a,所以由f(x)>f′(x)得ax2+3ax+1>2ax+3a,即有:ax2+ax+1-3a>0对一切x∈R恒成立,
设g(x)=ax2+ax+1-3a,
①当a=0时,g(x)=1>0恒成立,
②当a≠0时,若使g(x)=ax2+ax+1-3a>0恒成立,由g(x)=的对称轴x=
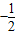 ,则有:
,则有: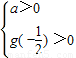 ,即
,即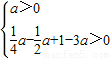 ,得
,得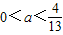 ,
,综合①②得实数a的取值范围是:
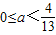
故应选:D
点评:本题考查一元二次不等式的应用,含参不等式的恒成立问题的求解,综合考查了利用函数的倒数来解决问题的能力,分类讨论和转化与化归思想的应用;对运算能力,思维能力亦有所要求.

练习册系列答案
相关题目