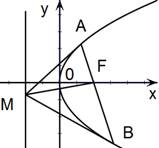
题目内容
(08年杨浦区测试)在等差数列![]() 中,公差
中,公差![]() ,且
,且![]() ,
,
(1)求![]() 的值.
的值.
(2)当![]() 时,在数列
时,在数列![]() 中是否存在一项
中是否存在一项![]() (
(![]() 正整数),使得
正整数),使得 ![]() ,
,![]() ,
,![]() 成等比数列,若存在,求
成等比数列,若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(3)若自然数![]() (
(![]() 为正整数)
为正整数)
满足![]() <
< ![]() <
<![]() <
< ![]() <
< ![]() <
<![]() , 使得
, 使得![]() 成等比数列,
成等比数列,
(文科考生做)当![]() 时, 用
时, 用![]() 表示
表示![]() .
.
(理科考生做)求![]() 的所有可能值.
的所有可能值.
解析:(1)在等差数列![]() 中,公差
中,公差![]() ,且
,且![]() ,
,
则![]() ……………………3分
……………………3分
(2)在等差数列![]() 中,公差
中,公差![]() ,且
,且![]() ,
,![]()
则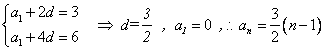
![]() …………5分
…………5分
又 ![]() 则 36=3am,
则 36=3am,![]() …………8分
…………8分
(文科)(3)在等差数列![]() 中,公差
中,公差![]() ,且
,且![]() ,
,![]()
则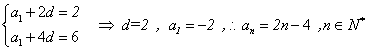 ……10分
……10分
又因为公比![]() 首项
首项![]() ,
,![]() …………14分
…………14分
又因为 ![]()
![]()
……………………16分
(理科)(3)![]()
![]()
![]() 成等比数列,
成等比数列,
![]()
![]()
∴![]() …………14分
…………14分
又∵![]() 成等比数列, ∴
成等比数列, ∴![]()
∴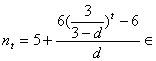 {6,7,8,9,10,…}对一切
{6,7,8,9,10,…}对一切![]() 成立,
成立,
∴![]() {2,3,4,5,…}(*),设
{2,3,4,5,…}(*),设![]() (
(![]() {2,3,4,5,…}),
{2,3,4,5,…}),
∴ ,(由二项式定理知,
,(由二项式定理知,
![]() 恒成立) ∴
恒成立) ∴![]() (
(![]() {2,3,4,5,…})
{2,3,4,5,…})
(注的证明可用无穷递降法完成,证略. ) ………………16分

练习册系列答案
相关题目