题目内容
平面直角坐标系xOy中,不同于原点O的动点P(x,y)满足|OP|2=|x|+|y|,则直线OP的斜率k的取值范围是
R
R
.分析:通过动点P(x,y)满足|OP|2=|x|+|y|,求出p的轨迹方程,然后求解直线OP的斜率k的取值范围.
解答: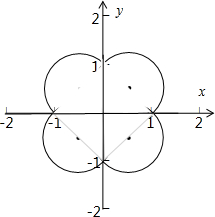 解:因为面直角坐标系xOy中,不同于O的动点P(x,y)满足|OP|2=|x|+|y|,
解:因为面直角坐标系xOy中,不同于O的动点P(x,y)满足|OP|2=|x|+|y|,
所以P的轨迹方程为:x2+y2=|x|+|y|,
即(|x|-
)2+(|y|-
)2=
.
满足点P的图形为:
所以直线OP的斜率k的取值范围是R.
故答案为:R.
 解:因为面直角坐标系xOy中,不同于O的动点P(x,y)满足|OP|2=|x|+|y|,
解:因为面直角坐标系xOy中,不同于O的动点P(x,y)满足|OP|2=|x|+|y|,所以P的轨迹方程为:x2+y2=|x|+|y|,
即(|x|-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
满足点P的图形为:
所以直线OP的斜率k的取值范围是R.
故答案为:R.
点评:本题考查曲线轨迹方程是求法,直线的斜率的范围,考查数形结合的思想.

练习册系列答案
相关题目
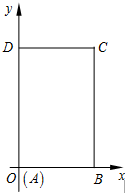 如图,在平面直角坐标系xOy中,已知矩形ABCD的两边AB,CD分别落在x轴、y轴的正半轴上,且AB=2,AD=4,点A与坐标原点重合.现将矩形折叠,使点A落在线段DC上,若折痕所在的直线的斜率为k,试写出折痕所在直线的方程及k的范围.
如图,在平面直角坐标系xOy中,已知矩形ABCD的两边AB,CD分别落在x轴、y轴的正半轴上,且AB=2,AD=4,点A与坐标原点重合.现将矩形折叠,使点A落在线段DC上,若折痕所在的直线的斜率为k,试写出折痕所在直线的方程及k的范围.