题目内容

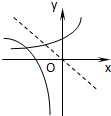
若函数在y=ax2+bx-c（-∞，0]是单调函数，则y=2ax+b的图象不可能是（　　）
A．B．C．D．
若函数y=ax2+bx-c为二次函数，则a≠0，二次函数的对称轴为x=-
b
2a
，要使在y=ax2+bx-c（-∞，0]是单调函数，则-
b
2a
≥0．
若a=0，则要使y=bx-c（-∞，0]是单调函数，则b≠0．
A中a=0，b＜0，显然满足条件．
B中，b＞0，2a＞0，不满足条件-
b
2a
≥0．
C中，2a＞0，b＜0，满足条件-
b
2a
≥0．
D中，2a＜0，b=0，满足条件-
b
2a
≥0．
所以只有B不可能．
故选B．
练习册系列答案
相关题目
若方程
1-x2
x+a
-1=0仅有一解，则实数a的取值范围是______．
设f(x)=
2-x
log81x
x∈(-∞，1]
x∈(1，+∞)
，则满足f(x)=
1
4
的x的值为______．
用二分法研究方程lnx+2x-6=0的一个近似解x=x0的问题．
（1）若借助计算器，算得
第一次：f（2）＜0，f（3）＞0⇒x0∈______；
第二次：______；
第三次：f（2.5）＜0，f（2.75）＞0⇒x0∈（2.5，2.75）；
第四次：f（2.5）＜0，f（2.625）＞0⇒x0∈（2.5，2.625）；
第五次：f（2.5）＜0，f（2.5625）＞0⇒x0∈（2.5，2.5625）；
第六次：f（2.53125）＜0，f（2.5625）＞0⇒x0∈（2.53125，2.5625）；
…
（2）若精确度为0.1，至少需算______次，近似解x0=______．
某市某家电制造集团在家电下乡运输中不断优化方案使运输效率（单位时间的运输量）逐步提高，则下列图中能反映实际的运输量Q随时间t变化的是（　　）
A．B．C．D．
当x在（-∞，+∞）上变化时，导函数f′（x）的符号变化如下表：
x（-∞.1）1（1，4）4（4，+∞）
f′（x）-0+0-
则函数f（x）的图象的大致形状为（　　）
A．B．C．D．
设函数y=f（x）的图象如图所示，则导函数y=f′（x）可能为（　　）
A．B．C．D．
设f（x）=2x-x2，则在下列区间中使函数f（x）有零点的区间是（　　）
A．[0，1]B．[1，2）C．[-2，-1]D．[-1，0]
已知a＞1，函数y=ax与y=loga（-x）的图象只可能是（　　）
A．B．C．D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网