题目内容
在某社区举办的《2008奥运知识有奖问答比赛》中,甲、乙、丙三人同时回答一道有关奥运知识的问题,已知甲回答这道题对的概率是
,甲、丙两人都回答错的概率是
,乙、丙两人都回答对的概率是
.
(Ⅰ)求乙、丙两人各自回答这道题对的概率;
(Ⅱ)用ξ表示回答该题对的人数,求ξ的分布列和数学期望Eξ.
| 3 |
| 4 |
| 1 |
| 12 |
| 1 |
| 4 |
(Ⅰ)求乙、丙两人各自回答这道题对的概率;
(Ⅱ)用ξ表示回答该题对的人数,求ξ的分布列和数学期望Eξ.
(Ⅰ)记“甲回答对这道题”、“乙回答对这道题”、“丙回答对这道题”分别为事件A、B、C,则P(A)=
,且有
,即
∴P(B)=
,P(C)=
.…6′
(Ⅱ)由(Ⅰ)P(
)=1-P(A)=
,P(
)=1-P(B)=
.ξ的可能取值为:0、1、2、3.
则P(ξ=0)=P(
•
•
)=
•
•
=
;P(ξ=1)=P(A•
•
)+P(
•B•
)+P(
•
•C)=
•
•
+
•
•
+
•
•
=
;P(ξ=2)=P(A•B•
)+P(A•
•C)+P(
•B•C)=
;P(ξ=3)=P(A•B•C)=
.…9′
∴ξ的分布列为
ξ的数学期望Eξ=0•
+1•
+2•
+3•
=
.…12′
| 3 |
| 4 |
|
|
∴P(B)=
| 3 |
| 8 |
| 2 |
| 3 |
(Ⅱ)由(Ⅰ)P(
| . |
| A |
| 1 |
| 4 |
| . |
| B |
| 1 |
| 3 |
则P(ξ=0)=P(
| . |
| A |
| . |
| B |
| . |
| C |
| 1 |
| 4 |
| 1 |
| 3 |
| 5 |
| 8 |
| 5 |
| 96 |
| . |
| B |
| . |
| C |
| . |
| A |
| . |
| C |
| . |
| A |
| . |
| B |
| 3 |
| 4 |
| 5 |
| 8 |
| 1 |
| 3 |
| 1 |
| 4 |
| 3 |
| 8 |
| 2 |
| 3 |
| 3 |
| 4 |
| 5 |
| 8 |
| 2 |
| 3 |
| 7 |
| 24 |
| . |
| C |
| . |
| B |
| . |
| A |
| 15 |
| 32 |
| 3 |
| 16 |
∴ξ的分布列为
| ξ | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 5 |
| 96 |
| 7 |
| 24 |
| 15 |
| 32 |
| 3 |
| 16 |
| 43 |
| 24 |

练习册系列答案
相关题目
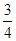 ,甲、丙两人都回答错的概率是
,甲、丙两人都回答错的概率是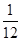 ,乙、丙两人都回答对的概率是
,乙、丙两人都回答对的概率是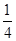 .
.