题目内容
在△ABC中,给出下列四个命题:①若sin2A=sin2B,则△ABC为等腰三角形;②若sinA=cosB,则△ABC是直角三角形;
③若cosA•cosB•cosC<0,则△ABC是钝角三角形;
④若cos(A-B)•cos(B-C)•cos(C-A)=1,则△ABC是等边三角形.
以上命题正确的是 (填命题序号).
【答案】分析:①若sin2A=sin2B,则 2A=2B,或 2A+2B=π,即A=B 或C=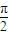 ,可知①不正确.
,可知①不正确.
②若sinA=cosB,找出∠A和∠B的反例,即可判断则△ABC是直角三角形错误,故②不正确.
③若cosA•cosB•cosC<0,cosA、cosB、cosC两个是正实数,一个是负数,故A、B、C中两个是锐角,一个是钝角,
故③正确.
④若cos(A-B)•cos(B-C)•cos(C-A)=1 可得 A=B=C,故△ABC是等边三角形,故④正确.
解答:解:①若sin2A=sin2B,则 2A=2B,或 2A+2B=π,即A=B 或C=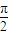 ,故△ABC为等腰三角形 或直角三角形,故①不正确.
,故△ABC为等腰三角形 或直角三角形,故①不正确.
②若sinA=cosB,例如∠A=100°和∠B=10°,满足sinA=cosB,,则△ABC不是直角三角形,故②不正确.
③若cosA•cosB•cosC<0,则由三角形各个内角的范围及内角和等于180° 知,cosA、cosB、cosC两个是正实数,
一个是负数,故A、B、C中两个是锐角,一个是钝角,故③正确.
④若cos(A-B)•cos(B-C)•cos(C-A)=1,则由三角形各个内角的范围及内角和等于180° 知,
cos(A-B)=cos(B-C)=cos(C-A)=1,故有 A=B=C,故△ABC是等边三角形,故④正确.
故答案为 ③④.
点评:本题考查判断三角形的形状的方法,注意角的范围及内角和等于180°,属于中档题.
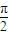 ,可知①不正确.
,可知①不正确.②若sinA=cosB,找出∠A和∠B的反例,即可判断则△ABC是直角三角形错误,故②不正确.
③若cosA•cosB•cosC<0,cosA、cosB、cosC两个是正实数,一个是负数,故A、B、C中两个是锐角,一个是钝角,
故③正确.
④若cos(A-B)•cos(B-C)•cos(C-A)=1 可得 A=B=C,故△ABC是等边三角形,故④正确.
解答:解:①若sin2A=sin2B,则 2A=2B,或 2A+2B=π,即A=B 或C=
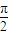 ,故△ABC为等腰三角形 或直角三角形,故①不正确.
,故△ABC为等腰三角形 或直角三角形,故①不正确.②若sinA=cosB,例如∠A=100°和∠B=10°,满足sinA=cosB,,则△ABC不是直角三角形,故②不正确.
③若cosA•cosB•cosC<0,则由三角形各个内角的范围及内角和等于180° 知,cosA、cosB、cosC两个是正实数,
一个是负数,故A、B、C中两个是锐角,一个是钝角,故③正确.
④若cos(A-B)•cos(B-C)•cos(C-A)=1,则由三角形各个内角的范围及内角和等于180° 知,
cos(A-B)=cos(B-C)=cos(C-A)=1,故有 A=B=C,故△ABC是等边三角形,故④正确.
故答案为 ③④.
点评:本题考查判断三角形的形状的方法,注意角的范围及内角和等于180°,属于中档题.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
在△ABC中,B(-2,0),C(2,0),A(x,y),给出△ABC满足的条件,就能得到动点A的轨迹方程,下表给出了一些条件及方程:
则满足条件①、②、③的轨迹方程分别为 (用代号C1、C2、C3填入).
则满足条件①、②、③的轨迹方程分别为
| 条 件 | 方 程 | ||||
| ①△ABC的周长为10 | C1:y2=25 | ||||
| ②△ABC的面积为10 | C2:x2+y2=4(y≠0) | ||||
| ③△ABC中,∠A=90° | C3:
|
在△ABC中,B(-2,0),C(2,0),A(x,y),给出△ABC满足的条件,就能得到动点A的轨迹方程,下表给出了一些条件及方程:
|
| A、C3、C1、C2 |
| B、C2、C1、C3 |
| C、C1、C3、C2 |
| D、C3、C2、C1 |
在△ABC中,A(x,y),B(-2,0),C(2,0),给出△ABC满足的条件,就能得到动点A的轨迹方程,下表给出了一些条件及方程:
则满足条件①、②、③的轨迹方程分别用代号表示为( )
A.E3,E1,E2
B.E1,E2,E3
C.E3,E2,E1
D.E1,E3,E2
| 条件 | 方程 |
| ①△ABC周长为10; ②△ABC面积为10; ③△ABC中,∠A=90° | E1:y2=25; E2:x2+y2=4(y≠0); E3: 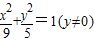 |
A.E3,E1,E2
B.E1,E2,E3
C.E3,E2,E1
D.E1,E3,E2
在△ABC中,B(-2,0),C(2,0),A(x,y),给出△ABC满足的条件,就能得到动点A的轨迹方程,下表给出了一些条件及方程:
则满足条件①、②、③的轨迹方程分别为 (用代号C1、C2、C3填入).
则满足条件①、②、③的轨迹方程分别为 (用代号C1、C2、C3填入).
| 条 件 | 方 程 |
| ①△ABC的周长为10 | C1:y2=25 |
| ②△ABC的面积为10 | C2:x2+y2=4(y≠0) |
| ③△ABC中,∠A=90° | C3: |