题目内容
(理)已知向量p∥q,其中p=(x+c-1,1),q=(ax2+1,y)(a,c,x,y∈R且a>0,x≠1-c),把其中x,y所满足的关系式记为y=f(x).若函数f(x)为奇函数,且当x>0时,f(x)有最小值(1)求函数f(x)的表达式;
(2)设数列{an},{bn}满足如下关系:an+1=![]() ,bn=
,bn=![]() (n∈N*),且b1=
(n∈N*),且b1=![]() ,求数列{bn}的通项公式,并求数列{(3n-1)
,求数列{bn}的通项公式,并求数列{(3n-1)![]() bn}(n∈N*)前n项的和Sn.
bn}(n∈N*)前n项的和Sn.
(文)已知等差数列{an}满足:an+1>an(n∈N*),a1=1,该数列的前三项分别加上1,1,3后顺次成为等比数列{bn}的前三项.
(1)分别求数列{an},{bn}的通项公式an,bn;
(2)设Tn=![]() (n∈N*),若Tn+
(n∈N*),若Tn+![]() <c(c∈Z)恒成立,求c的最小值.
<c(c∈Z)恒成立,求c的最小值.
答案:(理)解:(1)由p∥q,得y(x+c-1)=ax2+1.∴y=f(x)=![]() (a>0,x≠1-c).
(a>0,x≠1-c).
又函数f(x)为奇函数,有f(-x)=-f(x),可得c=1.当x>0时,f(x)=![]() =ax+
=ax+![]() .
.
∴![]() .∴a=2.故f(x)=
.∴a=2.故f(x)=![]() (x≠0).
(x≠0).
(2)an+1= ,
,
bn+1=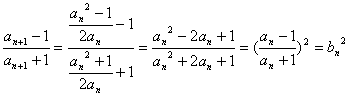 .
.
∴bn=bn-12=bn-24=…=![]() .
.
而b1=![]() ,∴bn=
,∴bn=![]() (n∈N*).
(n∈N*).
∴数列{(3n-1)![]() bn}的通项为(3n-1)
bn}的通项为(3n-1)![]() bn=(3n-1)·2n-1.
bn=(3n-1)·2n-1.
∴Sn=2·20+5·21+8·22+…+(3n-4)·2n-2+(3n-1)·2n-1.①
∴2Sn=2·21+5·22+8·23+…+(3n-4)·2n-1+(3n-1)·2n.②
①-②,得-Sn=2+3(21+22+…+2n-1)-(3n-1)2n.∴Sn=4+(3n-4)2n(n∈N*).
(文)解:(1)设d、q分别为数列{an}、{bn}的公差与公比,a1=1.
由题可知,a1=1,a2=1+d,a3=1+2d,分别加上1,1,3后得2,2+d,4+2d是等比数列{bn}的前三项,
∴(2+d)2=2(4+2d)![]() d=±2.
d=±2.
∵an+1>an,∴d>0.∴d=2.∴an=2n-1(n∈N*).
由此可得b1=2,b2=4,q=2,∴bn=2n(n∈N*).2分
(2)Tn=![]() ,①
,①
当n=1时,T1=![]() ;当n≥2时,
;当n≥2时,![]() Tn=
Tn=![]() .②
.②
①-②,得![]() Tn=
Tn=![]() .
.
∴Tn=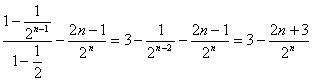 .
.
∴Tn+![]() =3
=3![]() <3.
<3.
∵(3![]() )在N*上是单调递增的,∴(3
)在N*上是单调递增的,∴(3![]() )∈[2,3).
)∈[2,3).
∴满足条件Tn+![]() <c(c∈Z)恒成立的最小整数值为c=3.
<c(c∈Z)恒成立的最小整数值为c=3.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 已知A(3,0)及双曲线E:
已知A(3,0)及双曲线E: