题目内容
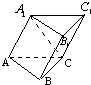 (2010•湖北模拟)如图,三棱柱ABC-A1B1C1的侧面A1ABB1⊥BC,且A1C与底面成45°角,AB=BC=2,则该棱柱体积的最小值为( )
(2010•湖北模拟)如图,三棱柱ABC-A1B1C1的侧面A1ABB1⊥BC,且A1C与底面成45°角,AB=BC=2,则该棱柱体积的最小值为( )分析:过A1作A1H⊥AB,垂足为H,连接HC,可以证出A1H⊥面ABC,A1H为三棱柱的高,∠A1HC为 A1C与底面成角,∠A1HC=45°,A1H为三棱柱的高与CH相等,而当CH⊥AB,即CH与CB重合时取得最小.
解答: 解:过A1作A1H⊥AB,垂足为H,连接HC,
解:过A1作A1H⊥AB,垂足为H,连接HC,
∵侧面A1ABB1⊥BC,A1H?面A1ABB1,∴BC⊥A1H,
∵AB∩BC=B,∴A1H⊥面ABC,
A1H为三棱柱的高.HC为A1C在底面上的射影,
∠A1HC为 A1C与底面成角,∠A1HC=45°,
∴△A1HC 为等腰直角三角形,A1H=CH,
当CH最小时,三棱柱的高最小,从而该棱柱体积最小.
而当CH⊥AB,即CH与CB重合时,取得最小值2
此时V=S△ABC×A1H=
×AB×BC×A1H=
×2×2×2=4
故选C.
 解:过A1作A1H⊥AB,垂足为H,连接HC,
解:过A1作A1H⊥AB,垂足为H,连接HC,∵侧面A1ABB1⊥BC,A1H?面A1ABB1,∴BC⊥A1H,
∵AB∩BC=B,∴A1H⊥面ABC,
A1H为三棱柱的高.HC为A1C在底面上的射影,
∠A1HC为 A1C与底面成角,∠A1HC=45°,
∴△A1HC 为等腰直角三角形,A1H=CH,
当CH最小时,三棱柱的高最小,从而该棱柱体积最小.
而当CH⊥AB,即CH与CB重合时,取得最小值2
此时V=S△ABC×A1H=
| 1 |
| 2 |
| 1 |
| 2 |
故选C.
点评:本题考查线面垂直关系的应用、判定.线面角的意义,体积的计算.考查空间想象能力、转化、计算、推理论证能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2010•湖北模拟)如图,正方体AC1的棱长为1,连接AC1,交平面A1BD于H,则以下命题中,错误的命题是( )
(2010•湖北模拟)如图,正方体AC1的棱长为1,连接AC1,交平面A1BD于H,则以下命题中,错误的命题是( ) (2010•湖北模拟)如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且PA=AB,点E是PD的中点.
(2010•湖北模拟)如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且PA=AB,点E是PD的中点.