ÌâÄżÄÚÈĘ
ĄŸÌâÄżĄż Ą°ÖĐčúÈËŸù¶ÁÊé4.3±ŸŁš°üÀšÍűÂçÎÄѧșÍœÌżÆÊ飩ŁŹ±Èș«čú”Ä11±ŸĄą·ščú”Ä20±ŸĄąÈŐ±Ÿ”Ä40±ŸĄąÓÌÌ«ÈË”Ä64±ŸÉÙ”Ă¶àŁŹÊÇÊÀœçÉÏÈËŸù¶ÁÊéŚîÉÙ”ÄčúŒÒĄŁĄ±ŐâžöÂ۶ϱ»žśÖÖĂœÌć·ŽžŽÒęÓĂĄŁłöÏÖŐâŃù”ÄÍłŒÆœáčûÎȚÒÉÊÇÁîÈËȚÏȚΔģŹ¶űÇÒșÍÆäËûčúŒÒÏà±ÈŁŹÎÒčúčúĂń”ÄÔĶÁÁżÈçŽËÖź”ÍŁŹÒČșÍÎÒčúŽ«ÍłÎÄĂśčĆčúĄąÀńÒÇÖź°î”Ä”ŰλȻÏà·û.ijХÇűÎȘÁËÌážßĐĄÇűÄÚÈËÔ±”ĶÁÊéĐËÈ€ŁŹÌŰŸÙ°ì¶ÁÊé»î¶ŻŁŹŚŒ±žčșœűÒ»¶šÁż”ÄÊéŒź·áž»ĐĄÇűÍŒÊéŐŸŁŹÓÉÓÚÄêÁä¶ÎȻ͏ĐèżŽČ»ÍŹÀàĐÍ”ÄÊéŒźŁŹÎȘÁËșÏÀíĆ䱞ŚÊÔŽŁŹ¶ÔĐĄÇűÄÚżŽÊéÈËÔ±œűĐĐÁËÄêÁä”Ä”śČ飏Ëæ»úłéÈĄÁËÒ»ÌìÖĐ![]() Ăû¶ÁÊéŐßœűĐĐ”śČ飏œ«ËûĂÇ”ÄÄêÁä·ÖłÉ6¶ÎŁș
Ăû¶ÁÊéŐßœűĐĐ”śČ飏œ«ËûĂÇ”ÄÄêÁä·ÖłÉ6¶ÎŁș![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() șó”Ă”œÈçÍŒËùÊŸ”ÄÆ”ÂÊ·ÖČŒÖ±·œÍŒŁźÎÊŁș
șó”Ă”œÈçÍŒËùÊŸ”ÄÆ”ÂÊ·ÖČŒÖ±·œÍŒŁźÎÊŁș
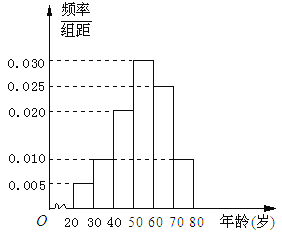
ŁšąńŁ©Çó40Ăû¶ÁÊéŐßÖĐÄêÁä·ÖČŒÔÚ![]() ”ÄÈËÊꣻ
”ÄÈËÊꣻ
ŁšąòŁ©Çó40Ăû¶ÁÊéŐßÄêÁä”ÄÖÚÊęșÍÖĐλÊę”ÄčÀŒÆÖ”Ł»ŁšÓĂžśŚéÇűŒäÖĐ”ăÖ”ŚśŽú±íŁ©
ŁšąóŁ©ÈôŽÓÄêÁäÔÚ![]() ”ĶÁÊéŐßÖĐÈÎÈĄ2ĂûŁŹÇóŐâÁœĂû¶ÁÊéŐßÖĐÄêÁäÔÚ
”ĶÁÊéŐßÖĐÈÎÈĄ2ĂûŁŹÇóŐâÁœĂû¶ÁÊéŐßÖĐÄêÁäÔÚ![]() ÇĄÓĐ1È˔ĞĆÂÊŁź
ÇĄÓĐ1È˔ĞĆÂÊŁź
ĄŸŽđ°žĄżŒûœâÎö
ĄŸœâÎöĄżŁš1Ł©ÓÉÆ”ÂÊ·ÖČŒÖ±·œÍŒÖȘÄêÁä·ÖČŒÔÚ![]() ”ÄÆ”ÂÊÎȘ
”ÄÆ”ÂÊÎȘ![]() ŁŹËùÒÔ40Ăû¶ÁÊéŐßÖĐÄêÁä·ÖČŒÔÚ
ŁŹËùÒÔ40Ăû¶ÁÊéŐßÖĐÄêÁä·ÖČŒÔÚ![]() ”ÄÈËÊęÎȘ
”ÄÈËÊęÎȘ![]() ŁšĂûŁ©ŁźĄĄĄĄĄĄĄĄ2·Ö
ŁšĂûŁ©ŁźĄĄĄĄĄĄĄĄ2·Ö
Łš2Ł©ÖÚÊę”ÄčÀŒÆÖ”ÎȘŚîžß”ÄŸŰĐΔÄÖД㣏ŒŽÖÚÊę”ÄčÀŒÆÖ””ÈÓÚ![]() ŁźĄĄĄĄĄĄĄĄ4·Ö
ŁźĄĄĄĄĄĄĄĄ4·Ö
ÉèÍŒÖĐœ«ËùÓĐŸŰĐÎĂæ»ęșÍŸù·Ö”ÄÄêÁäÎȘ![]() ŁŹÔò
ŁŹÔò![]() ŁŹœâ”Ă
ŁŹœâ”Ă![]() ŁŹŒŽÖĐλÊę”ÄčÀŒÆÖ”ÎȘ55ŁźĄĄĄĄĄĄĄĄ6·Ö
ŁŹŒŽÖĐλÊę”ÄčÀŒÆÖ”ÎȘ55ŁźĄĄĄĄĄĄĄĄ6·Ö
Łš3Ł©ÓÉÍŒżÉÖȘŁŹÄêÁäÔÚ![]() ”ĶÁÊéŐßÓĐ
”ĶÁÊéŐßÓĐ![]() ÈËŁŹÔÚ
ÈËŁŹÔÚ![]() ”ĶÁÊéŐßÓĐ
”ĶÁÊéŐßÓĐ![]() ÈËŁźÉèÄêÁäÔÚ
ÈËŁźÉèÄêÁäÔÚ![]() ”Ä2Ăû¶ÁÊéŐßÎȘ
”Ä2Ăû¶ÁÊéŐßÎȘ![]() ŁŹÄêÁäÔÚ
ŁŹÄêÁäÔÚ![]() ”Ä4Ăû¶ÁÊéŐßÎȘ
”Ä4Ăû¶ÁÊéŐßÎȘ![]() ŁŹÔòËùÓĐ»ù±ŸÊÂŒțÓĐŁș
ŁŹÔòËùÓĐ»ù±ŸÊÂŒțÓĐŁș![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ŁŹčČ15ÖÖŁŹÆäÖĐÄêÁäÔÚ
ŁŹčČ15ÖÖŁŹÆäÖĐÄêÁäÔÚ![]() ”ĶÁÊéŐßÇĄÓĐ1ÈË”ÄÊÂŒțÓĐŁș
”ĶÁÊéŐßÇĄÓĐ1ÈË”ÄÊÂŒțÓĐŁș![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ŁŹčČ8ÖÖŁŹËùÒÔŁŹŐâÁœĂû¶ÁÊéŐßÖĐÄêÁäÔÚ
ŁŹčČ8ÖÖŁŹËùÒÔŁŹŐâÁœĂû¶ÁÊéŐßÖĐÄêÁäÔÚ![]() ÇĄÓĐ1È˔ĞĆÂÊÎȘ
ÇĄÓĐ1È˔ĞĆÂÊÎȘ![]() ŁźĄĄĄĄĄĄĄĄ12·Ö
ŁźĄĄĄĄĄĄĄĄ12·Ö
ĄŸĂüÌâÒâÍŒĄż±ŸÌâÖśÒȘżŒČéÆ”ÂÊ·ÖČŒÖ±·œÍŒ”Äʶ±đÓëŒÆË㥹Ńù±Ÿ”ÄÊęŚÖÌŰŐśĄąčĆ”äžĆĐÍŁŹÒÔŒ°żŒČéʶ͌ÄÜÁŠĄąÉó¶ÁÄÜÁŠĄą»ńÈĄĐĆÏą”ÄÄÜÁŠĄą·ÖÀàÌÖÂÛËŒÏ룟

ĄŸÌâÄżĄżÄłÖĐѧÎȘÁËœâ2017œìžßÈęѧÉú”ÄĐÔ±đșÍÏČ°źÓÎÓŸÊÇ·ńÓĐčŰŁŹ¶Ô100ĂûžßÈęѧÉúœűĐĐÁËÎÊŸí”śČ飏”Ă”œÈçÏÂÁĐÁȘ±íŁș
ÏČ»¶ÓÎÓŸ | Č»ÏČ»¶ÓÎÓŸ | șÏŒÆ | |
ÄĐÉú | 10 | ||
ĆźÉú | 20 | ||
șÏŒÆ |
ÒŃÖȘÔÚŐâ100ÈËÖĐËæ»úłéÈĄ1ÈËŁŹłé”œÏČ»¶ÓÎÓŸ”ÄѧÉú”ÄžĆÂÊÎȘ![]() Łź
Łź
ŁšąńŁ©Ç뜫ÉÏÊöÁĐÁȘ±íČčłäÍêŐûŁ»
ŁšąòŁ©ĆжÏÊÇ·ńÓĐ99.9%”Ä°ŃÎŐÈÏÎȘÏČ»¶ÓÎÓŸÓëĐÔ±đÓĐčŰŁż
žœŁș 
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
ĄŸÌâÄżĄżÎȘŃĐŸżÄĐƟ͏ѧżŐŒäÏëÏóÄÜÁŠ”ÄČîÒìŁŹËïÀÏÊŠŽÓžßÒ»ÄꌶËæ»úŃĄÈĄÁË20ĂûÄĐÉúĄą20ĂûĆźÉúŁŹœűĐĐżŐŒäÍŒĐÎʶ±đČâÊÔŁŹ”Ă”œłÉŒšŸ„Ҷ͌ÈçÏÂŁŹŒÙ¶šłÉŒšŽóÓÚ”ÈÓÚ80·Ö”Ä͏ѧÎȘĄ°żŐŒäÏëÏóÄÜÁŠÍ»łöĄ±ŁŹ”ÍÓÚ80·Ö”Ä͏ѧÎȘĄ°żŐŒäÏëÏóÄÜÁŠŐ곣Ą±.

Łš1Ł©ÍêłÉÏÂĂæ![]() ÁĐÁȘ±íŁŹČąĆжÏÊÇ·ńÓĐ
ÁĐÁȘ±íŁŹČąĆжÏÊÇ·ńÓĐ![]() ”Ä°ŃÎŐÈÏÎȘĄ°żŐŒäÏëÏóÄÜÁŠÍ»łöĄ±ÓëĐÔ±đÓĐčŰŁ»
”Ä°ŃÎŐÈÏÎȘĄ°żŐŒäÏëÏóÄÜÁŠÍ»łöĄ±ÓëĐÔ±đÓĐčŰŁ»
żŐŒäÏëÏóÄÜÁŠÍ»łö | żŐŒäÏëÏóÄÜÁŠŐ곣 | șÏŒÆ | |
ÄĐÉú | |||
ĆźÉú | |||
șÏŒÆ |
Łš2Ł©ŽÓĄ°żŐŒäÏëÏóÄÜÁŠÍ»łöĄ±”Ä͏ѧÖĐËæ»úŃĄÈĄÄĐÉú2ĂûĄąĆźÉú2ĂûŁŹŒÇÆäÖĐłÉŒšłŹčę90·Ö”ÄÈËÊęÎȘ![]() ŁŹÇóËæ»ú±äÁż
ŁŹÇóËæ»ú±äÁż![]() ”Ä·ÖČŒÁĐșÍÊęѧÆÚÍû.
”Ä·ÖČŒÁĐșÍÊęѧÆÚÍû.
ÏÂĂæč«ÊœŒ°ÁÙœçÖ”±íœöč©ČÎżŒŁș 
| 0.100 | 0.050 | 0.010 | |
| 2.706 | 3.841 | 6.635 |