题目内容
设f(x)是一次函数,f(0)、f(3)、f(24)成等比数列,且f(0)>0,函数f(x)的图象与二次函数y=x2+6的图象有且只有一个公共点.
(Ⅰ)求f(x)的解析式:
(Ⅱ)设g(x)=mx2+4mx-f(x),若g(x)在区间[1,4]上是减函数,求实数m的取值范围.
解:(I)设f(x)=ax+b(a≠0)…
由题意可得[f(3)]2=f(0)•f(24)
即(3a+b)2=b•(24a+b)
整理:a=2b…①…
∵函数f(x)与y=x2+6图象有且只有一个公共点
∴ax+b=x2+6有两相等实根
即△=a2-4•(-b+6)=0
整理:a2+4b-24=0…②…
①②联立得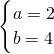 或
或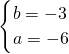
又∵f(0)>0,∴b>0故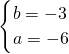 (舍)
(舍)
综上所述:f(x)=4x+2…
(Ⅱ)g(x)=mx2+4mx-f(x)=mx2+(4m-4)x-2
对称轴为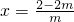
10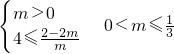 …
…
20 …
…
30 m=0时g(x)=-4x-2符合题意…
综上所述:m取值范围为 …
…
分析:(Ⅰ)由题意,可用待定系数法将一次函数解析式设为f(x)=ax+b(a≠0),由于f(0)、f(3)、f(24)成等比数列,由此可等到关于a,b的一个方程,又函数f(x)的图象与二次函数y=x2+6的图象有且只有一个公共点即由两者联立的方程组只有一个解,消元后利用判别式为0得到另一个关于a,b的方程,将两方程联立即可求得待定系数得到一次函数的解析式;
(II)由(I)可得g(x)=mx2+4mx-f(x)=mx2+(4m-4)x-2,可按二次项系数的符号分为两类,将g(x)在区间[1,4]上是减函数转化为关于实数m的不等式,分别解出实数m的取值范围再求三者的并集即可得到所求的答案
点评:本题考查函数与方程的应用,考查了待定系数法求解析式,二次函数的性质,考查了分类讨论的思想与转化的思想,本题综合性强,正确解题的关键是理解题意将问题正确转化,第二小题中分类讨论是本题的难点,易因为默认m为正数导致失根,转化时要考查全面
由题意可得[f(3)]2=f(0)•f(24)
即(3a+b)2=b•(24a+b)
整理:a=2b…①…
∵函数f(x)与y=x2+6图象有且只有一个公共点
∴ax+b=x2+6有两相等实根
即△=a2-4•(-b+6)=0
整理:a2+4b-24=0…②…
①②联立得
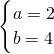 或
或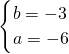
又∵f(0)>0,∴b>0故
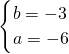 (舍)
(舍)综上所述:f(x)=4x+2…
(Ⅱ)g(x)=mx2+4mx-f(x)=mx2+(4m-4)x-2
对称轴为
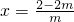
10
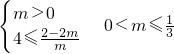 …
…20
 …
…30 m=0时g(x)=-4x-2符合题意…
综上所述:m取值范围为
 …
…分析:(Ⅰ)由题意,可用待定系数法将一次函数解析式设为f(x)=ax+b(a≠0),由于f(0)、f(3)、f(24)成等比数列,由此可等到关于a,b的一个方程,又函数f(x)的图象与二次函数y=x2+6的图象有且只有一个公共点即由两者联立的方程组只有一个解,消元后利用判别式为0得到另一个关于a,b的方程,将两方程联立即可求得待定系数得到一次函数的解析式;
(II)由(I)可得g(x)=mx2+4mx-f(x)=mx2+(4m-4)x-2,可按二次项系数的符号分为两类,将g(x)在区间[1,4]上是减函数转化为关于实数m的不等式,分别解出实数m的取值范围再求三者的并集即可得到所求的答案
点评:本题考查函数与方程的应用,考查了待定系数法求解析式,二次函数的性质,考查了分类讨论的思想与转化的思想,本题综合性强,正确解题的关键是理解题意将问题正确转化,第二小题中分类讨论是本题的难点,易因为默认m为正数导致失根,转化时要考查全面

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目