题目内容
给定区间(a,b),定义其区间长度为b-a.设f(x)是一次函数,且满足f(0)=-5,f[f(0)]=-15,若不等式f(x)f(m-x)>0的解集形成的区间长度为2,则实数m的所有可能取值为
3或7
3或7
.分析:先求出一次函数解析式,再利用不等式f(x)f(m-x)>0的解集形成的区间长度为2,建立方程,即可求得结论.
解答:解:设f(x)=kx+b,则
∵f(0)=-5,f[f(0)]=-15,
∴b=-5,k=2
∴f(x)=2x-5
∴不等式f(x)f(m-x)>0可化为(2x-5)(2x-2m+5)<0
∴(2x-5)(2x-2m+5)=0的根为
或
∵不等式f(x)f(m-x)>0的解集形成的区间长度为2,
∴|
-
|=2
∴m=3或7
故答案为:3或7
∵f(0)=-5,f[f(0)]=-15,
∴b=-5,k=2
∴f(x)=2x-5
∴不等式f(x)f(m-x)>0可化为(2x-5)(2x-2m+5)<0
∴(2x-5)(2x-2m+5)=0的根为
| 5 |
| 2 |
| 2m-5 |
| 2 |
∵不等式f(x)f(m-x)>0的解集形成的区间长度为2,
∴|
| 2m-5 |
| 2 |
| 5 |
| 2 |
∴m=3或7
故答案为:3或7
点评:本题考查函数解析式的确定,考查新定义,考查学生的计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 成立,求证:x唯一;
成立,求证:x唯一;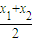 )和
)和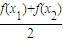 大小,并说明理由;
大小,并说明理由; 成立,求证:x唯一;
成立,求证:x唯一; )和
)和 大小,并说明理由;
大小,并说明理由;