题目内容
.函数f(x)=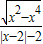 .给出函数f(x)下列性质:(1)f(x)的定义域和值域均为[-1,1];(2)f(x)是奇函数;(3)函数在定义域上单调递增;(4)函数f(x)有两零点;(5)A、B为函数f(x)图象上任意不同两点,则
.给出函数f(x)下列性质:(1)f(x)的定义域和值域均为[-1,1];(2)f(x)是奇函数;(3)函数在定义域上单调递增;(4)函数f(x)有两零点;(5)A、B为函数f(x)图象上任意不同两点,则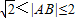 .则函数f(x)有关性质中正确描述的个数是( )
.则函数f(x)有关性质中正确描述的个数是( )A.1
B.2
C.3
D.4
【答案】分析:求出函数的定义域,化简函数的解析式,作出函数图象,根据函数的图象判断所给性质的正误.
解答:解:∵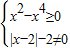 ∴函数定义域为
∴函数定义域为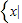 -1≤x<0或0<x≤1,}
-1≤x<0或0<x≤1,}
∴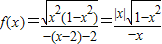 =
=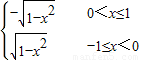
作出函数图象,如图所示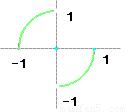
由图象可知函数定义域为[-1,0)∪(0,1],值域为(-1,1)故(1)不正确;
∵函数定义域关于原点对称且
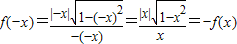
∴函数f(x)为奇函数,故(2)正确;
由图象可知函数在[-1,0)上为单调增函数,在(0,1]上也是单调增函数,但在定义域上不是增函数,如-1<1,但f(-1)>f(1).故(3)不正确;
由图象可知函数的零点为x=-1,x=1,故(4)正确;
由图象可知图象为两个四分之一个圆弧构成,且半径为1,最大为AB连线过原点时最大为2,最小为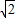 ,但取不到.
,但取不到.
故(5)正确.
故选C.
点评:本题主要考查了函数的性质、函数的图象,并利用函数的图象研究函数的性质,体现了数形结合在数学解题中的应用.
解答:解:∵
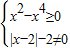 ∴函数定义域为
∴函数定义域为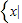 -1≤x<0或0<x≤1,}
-1≤x<0或0<x≤1,}∴
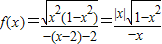 =
=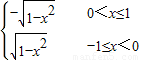
作出函数图象,如图所示

由图象可知函数定义域为[-1,0)∪(0,1],值域为(-1,1)故(1)不正确;
∵函数定义域关于原点对称且
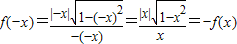
∴函数f(x)为奇函数,故(2)正确;
由图象可知函数在[-1,0)上为单调增函数,在(0,1]上也是单调增函数,但在定义域上不是增函数,如-1<1,但f(-1)>f(1).故(3)不正确;
由图象可知函数的零点为x=-1,x=1,故(4)正确;
由图象可知图象为两个四分之一个圆弧构成,且半径为1,最大为AB连线过原点时最大为2,最小为
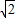 ,但取不到.
,但取不到.故(5)正确.
故选C.
点评:本题主要考查了函数的性质、函数的图象,并利用函数的图象研究函数的性质,体现了数形结合在数学解题中的应用.

练习册系列答案
 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目