题目内容
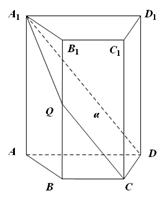
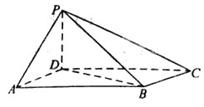
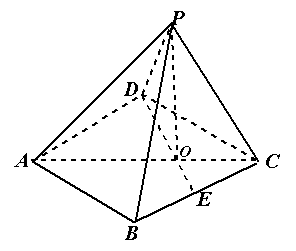
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.
(1)证明:PA⊥BD;
(2)若PD=AD,求二面角A-PB-C的余弦值。

(1)证明:PA⊥BD;
(2)若PD=AD,求二面角A-PB-C的余弦值。
(1)见解析 (2)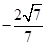
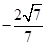
(1)因为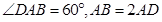 , 由余弦定理得
, 由余弦定理得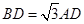
从而BD2+AD2= AB2,故BD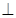 AD;又PD
AD;又PD 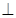 底面ABCD,可得BD
底面ABCD,可得BD 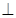 PD
PD
所以BD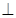 平面PAD. 故 PA
平面PAD. 故 PA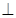 BD
BD
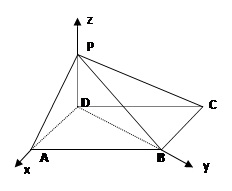
(2)如图,以D为坐标原点,AD的长为单位长,射线DA为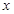 轴的正半轴建立空间直角坐标系D-
轴的正半轴建立空间直角坐标系D-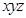 ,则
,则
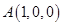 ,
,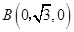 ,
,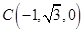 ,
,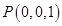 。
。
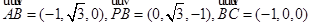
设平面PAB的法向量为n=(x,y,z),则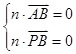 ,
,
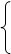 即
即 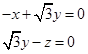
因此可取n=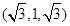
设平面PBC的法向量为m,则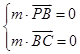
可取m=(0,-1,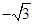 )
) 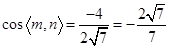
故二面角A-PB-C的余弦值为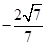
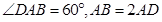 , 由余弦定理得
, 由余弦定理得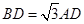
从而BD2+AD2= AB2,故BD
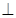 AD;又PD
AD;又PD 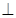 底面ABCD,可得BD
底面ABCD,可得BD 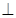 PD
PD所以BD
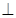 平面PAD. 故 PA
平面PAD. 故 PA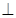 BD
BD(2)如图,以D为坐标原点,AD的长为单位长,射线DA为
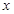 轴的正半轴建立空间直角坐标系D-
轴的正半轴建立空间直角坐标系D-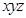 ,则
,则
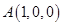 ,
,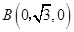 ,
,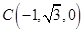 ,
,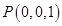 。
。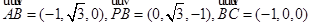
设平面PAB的法向量为n=(x,y,z),则
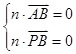 ,
,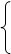 即
即 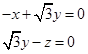
因此可取n=
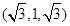
设平面PBC的法向量为m,则
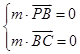
可取m=(0,-1,
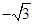 )
) 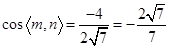
故二面角A-PB-C的余弦值为
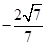

练习册系列答案
相关题目
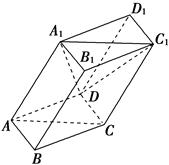
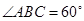 ,平面
,平面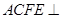 平面ABCD,四边形ACFE是矩形,AE=a.
平面ABCD,四边形ACFE是矩形,AE=a. 平面ACFE;
平面ACFE;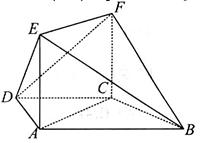
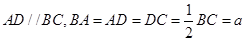 ,E是BC的中点,将△BAE沿AE翻折成
,E是BC的中点,将△BAE沿AE翻折成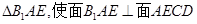 ,F为
,F为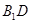 的中点.
的中点.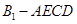 的体积;
的体积;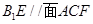 ;
; 所成锐二面角的余弦值.
所成锐二面角的余弦值.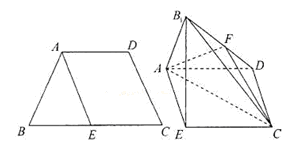
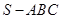 中,
中,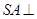 底面
底面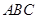 ,点
,点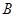 为以
为以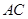 为直径的圆上任意一动点,且
为直径的圆上任意一动点,且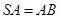 ,点
,点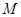 是
是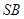 的中点,
的中点,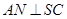 且交
且交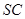 于点
于点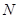 .
.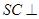 面
面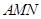 ;
;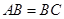 时,求二面角
时,求二面角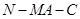 的余弦值.
的余弦值.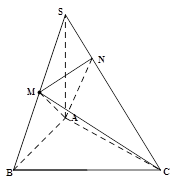
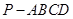 的底面的菱形,
的底面的菱形,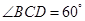 ,点
,点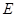 是
是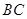 边的中点,
边的中点,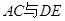 交于点
交于点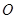 ,
,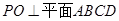
 ;
;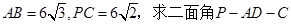 的大小;
的大小;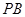 与
与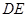 所成角的余弦值。
所成角的余弦值。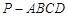 的底面为直角梯形,
的底面为直角梯形,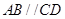 ,
,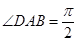 ,
, 底面
底面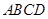 ,且
,且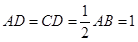 ,
,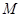 是
是 的中点.
的中点. 平面
平面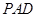 ;
;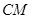 与平面
与平面 所成的角为
所成的角为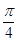 ,求二面角
,求二面角 的余弦值.
的余弦值.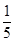
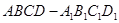 中,
中,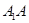
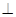 底面
底面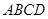 .四边形
.四边形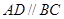 ,且
,且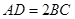 .过
.过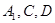 三点的平面记为
三点的平面记为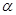 ,
,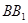 与
与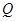 .
.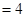 ,
,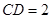 ,梯形
,梯形