题目内容
已知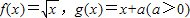 ,设
,设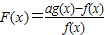
(1)当a=4时,求F(x)的最小值
(2)当1≤x≤4时,不等式F(x)>1恒成立,求a的取值范围.
【答案】分析:(1)把a=4代入到F(x)中化简得到F(x)的解析式利用基本功不等式求出F(x)的最小值即可;
(2)可设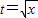 ,
,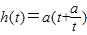 ,F(x)>1在x∈[1,4]上恒成立,则只需h(t)在[1,2]上的最小值大于2,由函数
,F(x)>1在x∈[1,4]上恒成立,则只需h(t)在[1,2]上的最小值大于2,由函数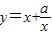 的单调性求最值的方法求出最值即可列出关于a的不等式,求出解集即可.
的单调性求最值的方法求出最值即可列出关于a的不等式,求出解集即可.
解答:解:(1)当a=4时,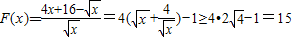 ∴
∴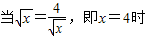 ,F(x)min=15(4分)
,F(x)min=15(4分)
(2)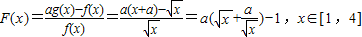 (6分)
(6分)
设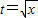 ,则
,则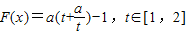 ,令
,令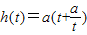 ∵F(x)>1在x∈[1,4]上恒成立,则只需h(t)在[1,2]上的最小值大于2,由函数
∵F(x)>1在x∈[1,4]上恒成立,则只需h(t)在[1,2]上的最小值大于2,由函数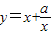 的单调性知
的单调性知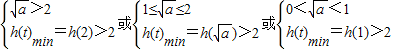
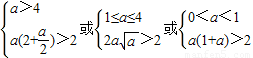 ,解得a>1(12分)
,解得a>1(12分)
点评:考查学生基本不等式在最值问题中的应用、利用整体代换的数学思想解决数学问题的能力,以及不等式恒成立的证明方法.
(2)可设
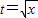 ,
,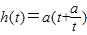 ,F(x)>1在x∈[1,4]上恒成立,则只需h(t)在[1,2]上的最小值大于2,由函数
,F(x)>1在x∈[1,4]上恒成立,则只需h(t)在[1,2]上的最小值大于2,由函数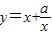 的单调性求最值的方法求出最值即可列出关于a的不等式,求出解集即可.
的单调性求最值的方法求出最值即可列出关于a的不等式,求出解集即可.解答:解:(1)当a=4时,
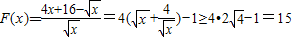 ∴
∴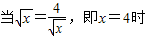 ,F(x)min=15(4分)
,F(x)min=15(4分)(2)
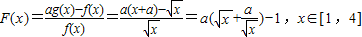 (6分)
(6分)设
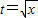 ,则
,则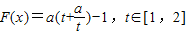 ,令
,令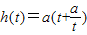 ∵F(x)>1在x∈[1,4]上恒成立,则只需h(t)在[1,2]上的最小值大于2,由函数
∵F(x)>1在x∈[1,4]上恒成立,则只需h(t)在[1,2]上的最小值大于2,由函数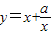 的单调性知
的单调性知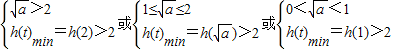
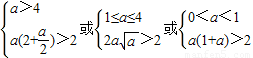 ,解得a>1(12分)
,解得a>1(12分)点评:考查学生基本不等式在最值问题中的应用、利用整体代换的数学思想解决数学问题的能力,以及不等式恒成立的证明方法.

练习册系列答案
相关题目
 .
. 的极小值;
的极小值; ,x∈[-1,1],求
,x∈[-1,1],求 的最大值F(a).
的最大值F(a). .
. 的极小值;
的极小值; ,x∈[-1,1],求
,x∈[-1,1],求 的最大值F(a).
的最大值F(a).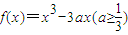 .
.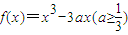 .
.