题目内容
小明家是否参加某一理财项目,由爸爸、妈妈和小明三人投票决定,他们三人都有“参加“、“中立“、“反对”三种票各一张,投票时,每人必须且只能投-张,每人投三种票中的任何一张的概率都为| 1 | 3 |
(1)求小明家参加该理财项目的概率.
(2)设投票结果中“中立”粟的张数为随机变量ξ,求ξ的分布列及数学期望.
分析:(1)三人的投票相互没有影响,每一个人的投票可以看做一次独立重复试验,小明家参加该理财项目包括两种情况,且这两种情况是互斥的,得到概率.
(2)由题意得到变量的可能取值,结合变量对应的事件,写出变量对应的概率,写出分布列和期望值.
(2)由题意得到变量的可能取值,结合变量对应的事件,写出变量对应的概率,写出分布列和期望值.
解答:解:(1)每人投三种票中的任何一张的概率都为
,
他们三人的投票相互没有影响,
∴每一个人的投票可以看做一次独立重复试验,
小明家参加该理财项目包括两种情况.且这两种情况是互斥的,
∴P=
(
)2(
) +
(
)3=
(2)由题意知变量ξ的可能取值是0,1,2,3
P(ξ=0)=(
)3=
P(ξ=1)=
×
×(
)2=
P(ξ=2)=
×
×(
)2=
P(ξ=3)=
(
)3=
∴分布列是
∴Eξ=0×
+1×
+2×
+3×
=1
| 1 |
| 3 |
他们三人的投票相互没有影响,
∴每一个人的投票可以看做一次独立重复试验,
小明家参加该理财项目包括两种情况.且这两种情况是互斥的,
∴P=
| C | 2 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| C | 3 3 |
| 1 |
| 3 |
| 7 |
| 27 |
(2)由题意知变量ξ的可能取值是0,1,2,3
P(ξ=0)=(
| 2 |
| 3 |
| 8 |
| 27 |
P(ξ=1)=
| C | 1 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 4 |
| 9 |
P(ξ=2)=
| C | 2 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 9 |
P(ξ=3)=
| C | 3 3 |
| 1 |
| 3 |
| 1 |
| 27 |
∴分布列是
| ξ | 0 | 1 | 2 | 3 | ||||||||
| p |
|
|
|
|
| 8 |
| 27 |
| 4 |
| 9 |
| 2 |
| 9 |
| 1 |
| 27 |
点评:本题考查离散型随机变量的分布列和期望,本题解题的关键是写出分布列中变量的概率,注意模仿上一问做出的结果

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案
相关题目
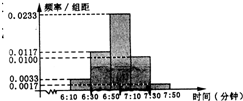 (2012•莆田模拟)小明家订了一份《湄洲日报》,暑假期间他收集了每天报纸送达的时间的数据,并绘制成频率分布直方图如图所示.
(2012•莆田模拟)小明家订了一份《湄洲日报》,暑假期间他收集了每天报纸送达的时间的数据,并绘制成频率分布直方图如图所示. ,他们三人的投票相互没有影响,规定:若投票结果中至少有两张“参加“票,则决定参加该理财项目;否则,放弃该理财项目.
,他们三人的投票相互没有影响,规定:若投票结果中至少有两张“参加“票,则决定参加该理财项目;否则,放弃该理财项目. ,他们三人的投票相互没有影响,规定:若投票结果中至少有两张“参加“票,则决定参加该理财项目;否则,放弃该理财项目.
,他们三人的投票相互没有影响,规定:若投票结果中至少有两张“参加“票,则决定参加该理财项目;否则,放弃该理财项目.