题目内容
设α、β都是锐角,且cosα=
,sin(α+β)=
,则cosβ=
.
| ||
| 5 |
| 3 |
| 5 |
2
| ||
| 25 |
2
| ||
| 25 |
分析:由α为锐角,根据cosα的值,求出sinα的值,利用两角和与差的正弦函数公式化简sin(α+β),且根据其值范围确定出α+β的范围,利用同角三角函数间的基本关系求出cos(α+β)的值,所求式子中的角β变形为(α+β)-α,利用两角和与差的余弦函数公式化简,将各自的值代入计算即可求出值.
解答:解:∵α为锐角,cosα=
<
,
∴sinα=
=
,
∵sin(α+β)=sinαcosβ+cosαsinβ=
(2cosβ+sinβ)=
,且
<
<
,
∴2cosβ+sinβ=
①,且
<α+β<π,
∴cos(α+β)=-
=-
,
则cosβ=cos[(α+β)-α]=cos(α+β)cosα+sin(α+β)sinα=-
×
+
×
=
.
故答案为:
| ||
| 5 |
| ||
| 2 |
∴sinα=
| 1-cos2α |
2
| ||
| 5 |
∵sin(α+β)=sinαcosβ+cosαsinβ=
| ||
| 5 |
| 3 |
| 5 |
| 1 |
| 2 |
| 3 |
| 5 |
| ||
| 2 |
∴2cosβ+sinβ=
3
| ||
| 5 |
| π |
| 2 |
∴cos(α+β)=-
| 1-sin2(α+β) |
| 4 |
| 5 |
则cosβ=cos[(α+β)-α]=cos(α+β)cosα+sin(α+β)sinα=-
| 4 |
| 5 |
| ||
| 5 |
| 3 |
| 5 |
2
| ||
| 5 |
2
| ||
| 25 |
故答案为:
2
| ||
| 25 |
点评:此题考查了两角和与差的正弦、余弦函数公式,以及同角三角函数间的基本关系,熟练掌握公式是解本题的关键.

练习册系列答案
相关题目
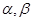 都是锐角,且
都是锐角,且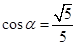 ,
,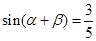 则
则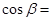 ( )
( )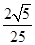 B.
B.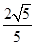 C.
C.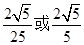 D.
D.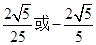
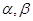 都是锐角,且
都是锐角,且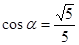 ,
,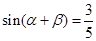 ,则
,则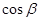 =( )
=( )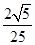 B.
B.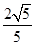 C.
C.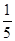 或
或