题目内容
下列命题中,真命题个数为( )
①直线2x+y-1=0的一个方向向量为
=(1,-2);
②直线x+y-1=0平分圆x2+y2-2y=1;
③曲线
+
=1表示椭圆的充要条件为-1<m<6;
④如果双曲线
-
=1上一点P到双曲线右焦点距离为2,则点P到y轴的距离是
.
①直线2x+y-1=0的一个方向向量为
| a |
②直线x+y-1=0平分圆x2+y2-2y=1;
③曲线
| x2 |
| m+1 |
| y2 |
| 6-m |
④如果双曲线
| x2 |
| 4 |
| y2 |
| 2 |
2
| ||
| 3 |
分析:对于①直线2x+y-1=0的一个方向向量为
=(1,-2);②直线x+y-1=0经过圆x2+y2-2y=1的圆心(0,1);③曲线
+
=1表示椭圆的充要条件为-1<m<6且m≠
,;对于④根据点P到双曲线右焦点的距离判断点P在右支上,再根据双曲线的第二定义知点P到双曲线右准线的距离和有准线方程,进而得到点P到y轴的距离.
| a |
| x2 |
| m+1 |
| y2 |
| 6-m |
| 5 |
| 2 |
解答:解:①直线2x+y-1=0的一个方向向量为
=(1,-2);正确;
②直线x+y-1=0经过圆x2+y2-2y=1的圆心(0,1)故平分圆x2+y2-2y=1;正确;
③曲线
+
=1表示椭圆的充要条件为-1<m<6且m≠
,故错;
对于④由点P到双曲线右焦点 (
,0)的距离是2知P在双曲线右支上.
又由双曲线的第二定义知点P到双曲线右准线的距离是
,双曲线的右准线方程是 x=
,
故点P到y轴的距离是
;错.
故选B.
| a |
②直线x+y-1=0经过圆x2+y2-2y=1的圆心(0,1)故平分圆x2+y2-2y=1;正确;
③曲线
| x2 |
| m+1 |
| y2 |
| 6-m |
| 5 |
| 2 |
对于④由点P到双曲线右焦点 (
| 6 |
又由双曲线的第二定义知点P到双曲线右准线的距离是
2
| ||
| 3 |
2
| ||
| 3 |
故点P到y轴的距离是
4
| ||
| 3 |
故选B.
点评:本题主要考查了方向向量、椭圆的方程、双曲线的简单性质等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
相关题目
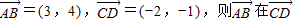 上的投影为-2;
上的投影为-2;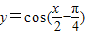 的图象,只需将
的图象,只需将 的图象向左平移
的图象向左平移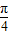 个单位.
个单位.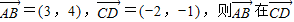 上的投影为-2;
上的投影为-2;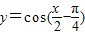 的图象,只需将
的图象,只需将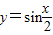 的图象向左平移
的图象向左平移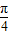 个单位.
个单位.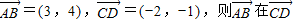 上的投影为-2;
上的投影为-2;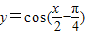 的图象,只需将
的图象,只需将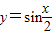 的图象向左平移
的图象向左平移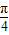 个单位.
个单位.