题目内容
求函数y=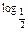 (4x-x2)的单调区间.
(4x-x2)的单调区间.
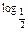 (4x-x2)的单调区间.
(4x-x2)的单调区间.函数y=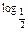 (4x-x2)的单调减区间是(0,2],单调增区间是[2,4)
(4x-x2)的单调减区间是(0,2],单调增区间是[2,4)
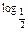 (4x-x2)的单调减区间是(0,2],单调增区间是[2,4)
(4x-x2)的单调减区间是(0,2],单调增区间是[2,4)由4x-x2>0,得函数的定义域是(0,4).令t=4x-x2,则y= 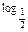 t.
t.
∵t=4x-x2=-(x-2)2+4,∴t=4x-x2的单调减区间是[2,4),增区间是(0,2].
又y=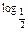 t在(0,+∞)上是减函数,
t在(0,+∞)上是减函数,
∴函数y=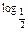 (4x-x2)的单调减区间是(0,2],单调增区间是[2,4).
(4x-x2)的单调减区间是(0,2],单调增区间是[2,4).
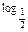 t.
t.∵t=4x-x2=-(x-2)2+4,∴t=4x-x2的单调减区间是[2,4),增区间是(0,2].
又y=
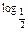 t在(0,+∞)上是减函数,
t在(0,+∞)上是减函数,∴函数y=
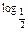 (4x-x2)的单调减区间是(0,2],单调增区间是[2,4).
(4x-x2)的单调减区间是(0,2],单调增区间是[2,4).
练习册系列答案
相关题目
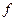 (
(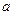 *b)=
*b)=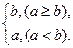 则函数
则函数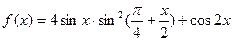
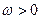 为常数,若
为常数,若 上是增函数,求
上是增函数,求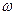 的取值范围
的取值范围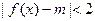 成立的充分条件是
成立的充分条件是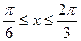 ,求实数m的取值范围
,求实数m的取值范围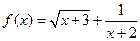 ,
,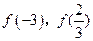 的值;
的值;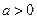 时,求
时,求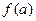 ,
,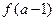 的值.
的值.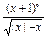 的定义域:
的定义域: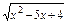 ;
;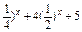 .
. 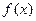 在
在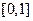 上有定义,要使函数
上有定义,要使函数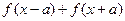 有定义,则a的取值范围为( )
有定义,则a的取值范围为( ) ;
; ;
; ;
;
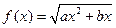 ,存在一个正数
,存在一个正数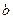 ,使得
,使得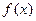 的定义域和值域相同,则非零实数
的定义域和值域相同,则非零实数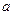 的值为__________.
的值为__________.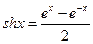 ,双曲余弦函数:
,双曲余弦函数: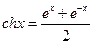 ,则函数
,则函数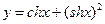 的值域为 .
的值域为 .