题目内容
α、β、γ为两两不重合的平面,l、m、n为两两不重合的直线,给出下列四个命题
①若α⊥γ,β⊥γ,则α∥β
②若m∥β,n∥β,则α∥β
③l?α,α∥β,则l∥β
④若α∩β=γ,β∩γ=m,γ∩α=n,l∥m,则m∥n
其中正确命题的个数为
①若α⊥γ,β⊥γ,则α∥β
②若m∥β,n∥β,则α∥β
③l?α,α∥β,则l∥β
④若α∩β=γ,β∩γ=m,γ∩α=n,l∥m,则m∥n
其中正确命题的个数为
2
2
.分析:对于①可列举正方体进行说明,对于②对照面面平行的判定定理进行判定,对于③根据面面平行的性质进行判定,对于④根据线面平行的性质进行判定即可.
解答:解:①若α⊥γ,β⊥γ,则α∥β,如正方体共顶点的三个平面就不成立,故不正确;
②若m∥β,n∥β,则α∥β,对照面面平行的判定定理可知不正确;
③l?α,α∥β,则l∥β,根据面面平行的性质可知该命题正确;
④若α∩β=γ,β∩γ=m,γ∩α=n,l∥m,则m∥n,如三棱柱符合条件,根据线面平行的性质可知正确
故答案为:2
②若m∥β,n∥β,则α∥β,对照面面平行的判定定理可知不正确;
③l?α,α∥β,则l∥β,根据面面平行的性质可知该命题正确;
④若α∩β=γ,β∩γ=m,γ∩α=n,l∥m,则m∥n,如三棱柱符合条件,根据线面平行的性质可知正确
故答案为:2
点评:本题主要考查了空间两直线的位置关系,以及线面、面面位置关系等有关知识,同时考查了对定理的理解,属于综合题.

练习册系列答案
相关题目
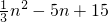 (克),如果满足f(n)>n,则称该球为重球.这些球以等可能性(不受重量和号码的影响)从袋里取出.
(克),如果满足f(n)>n,则称该球为重球.这些球以等可能性(不受重量和号码的影响)从袋里取出.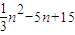 (克),如果满足f(n)>n,则称该球为重球.这些球以等可能性(不受重量和号码的影响)从袋里取出.
(克),如果满足f(n)>n,则称该球为重球.这些球以等可能性(不受重量和号码的影响)从袋里取出.