题目内容
袋里装由20个球,每个球上都记有1到20的一个号码,设号码为n的球重为f(n)=| 1 | 3 |
(1)如果任意取出1球,试求该球为重球的概率;
(2)如果同时任意取出两个球,试求它们重量相等的概率.
分析:(1)本题是一个古典概型,试验发生包含的事件是任取1个球,共有20个等可能的结果,满足条件f(n)>n,解关于n的一元二次不等式,得到n的范围,看出n的个数,得到概率.
(2)本题是一个古典概型,试验发生包含的事件是任取两个球共有C202种等可能的取法,满足条件的事件是它们重量相等,写出关于n的方程,根据条件得到n之间的关系,得到符合条件的事件数,得到概率.
(2)本题是一个古典概型,试验发生包含的事件是任取两个球共有C202种等可能的取法,满足条件的事件是它们重量相等,写出关于n的方程,根据条件得到n之间的关系,得到符合条件的事件数,得到概率.
解答:解:(1)由题意知本题是一个古典概型,
试验发生包含的事件是任取1个球,共有20个等可能的结果,
由
n2-5n+15>n,
即n2-18n+45>0,
∴n<3或n>15.
因此球的重量大于其号码数的结果为7种,
∴概率为:
.
(2)由题意知本题是一个古典概型,
试验发生包含的事件是任取两个球共有C202=190种等可能的取法.
f(n1)=f(n2)(n1≠n2),
则
-5n1+15=
-5n2+15,
即
(n1-n2)(n1+n2)=5(n1-n2).
因为n1≠n2,
∴n1+n2=15.
由此可见,任取2个球且重量相同的取法有7种,
∴所求概率为:P=
=
.
试验发生包含的事件是任取1个球,共有20个等可能的结果,
由
| 1 |
| 3 |
即n2-18n+45>0,
∴n<3或n>15.
因此球的重量大于其号码数的结果为7种,
∴概率为:
| 7 |
| 20 |
(2)由题意知本题是一个古典概型,
试验发生包含的事件是任取两个球共有C202=190种等可能的取法.
f(n1)=f(n2)(n1≠n2),
则
| n 12 |
| 3 |
| n22 |
| 3 |
即
| 1 |
| 3 |
因为n1≠n2,
∴n1+n2=15.
由此可见,任取2个球且重量相同的取法有7种,
∴所求概率为:P=
| 7 | ||
|
| 7 |
| 190 |
点评:本题考查古典概型,考查一元二次不等式的解法,是一个综合题,这种问题是以古典概型为载体,实际上考查的是其他的知识点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
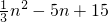 (克),如果满足f(n)>n,则称该球为重球.这些球以等可能性(不受重量和号码的影响)从袋里取出.
(克),如果满足f(n)>n,则称该球为重球.这些球以等可能性(不受重量和号码的影响)从袋里取出.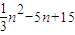 (克),如果满足f(n)>n,则称该球为重球.这些球以等可能性(不受重量和号码的影响)从袋里取出.
(克),如果满足f(n)>n,则称该球为重球.这些球以等可能性(不受重量和号码的影响)从袋里取出.