题目内容
15.已知a、b为实数,集合M={b,1},N={a,0},f:x→x表示把M中的元素x映射到集合N中仍为x,则a+b等于( )| A. | -1 | B. | 2 | C. | 1 | D. | 1或2 |
分析 由题目给出的映射的概念,可知b→0,1→a,由此求出a,b的值,则答案可求
解答 解:由集合M={b,1},N={a,0},且f:x→x,
∴b→0,1→a,
则a=1,b=0.
则a+b=1.
故选:C.
点评 本题考查了映射的概念,考查了集合中元素的特性,是基础的概念题.

练习册系列答案
 目标测试系列答案
目标测试系列答案
相关题目
6.已知命题p:y=sin(2x+$\frac{π}{3}$)的图象关于(-$\frac{π}{6}$,0)对称;命题q:若2a<2b,则lga<lgb.则下列命题中正确的是( )
| A. | p∧q | B. | ?p∧q | C. | p∧?q | D. | ?p∨q |
3.函数f(x)=-2x+3,x∈[-2,3)的值域是( )
| A. | [-1,3) | B. | [-3,7) | C. | (-1,3] | D. | (-3,7] |
10.函数f(x)=$\frac{\root{3}{x-4}}{a{x}^{2}+4ax+3}$的定义域为R,那么实数a的取值范围是( )
| A. | [0.$\frac{3}{4}$) | B. | (0,$\frac{3}{4}$) | C. | (-$\frac{3}{4}$,+∞) | D. | (-∞,+∞) |
7.已知数列{an}的前n项和Sn=2n(n∈N*),则n≥2时,a12+a22+…+an2=( )
| A. | $\frac{1}{3}({4^n}-1)$ | B. | $\frac{1}{3}({4^n}+8)$ | C. | $\frac{1}{3}{({2^n}-1)^2}$ | D. | $\frac{1}{3}{({2^n}+4)^2}$ |
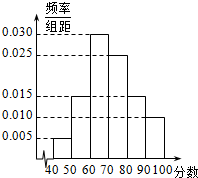 某校高二年级共有学生600名,从某次测试成绩中随机抽出50名同学的成绩,形成样本频率分布直方图如右上,据此估计全年级成绩不少于60分的人数为480.
某校高二年级共有学生600名,从某次测试成绩中随机抽出50名同学的成绩,形成样本频率分布直方图如右上,据此估计全年级成绩不少于60分的人数为480.