题目内容
对于数列A:a1,a2,…,an,若满足ai∈{0,1}(i=1,2,3,…,n),则称数列A为“0-1数列”.定义变换T,T将“0-1数列”A中原有的每个1都变成0,1,原有的每个0都变成1,0.例如A:1,0,1,则T(A):0,1,1,0,0,1.设A是“0-1数列”,令Ak=T(Ak-1),k=1,2,3,…(1)若数列A2:1,0,0,1,0,1,1,0,1,0,0,1.则数列A为 ;
(2)若A为0,1,记数列Ak中连续两项都是0的数对个数为lk,k=1,2,3,…,则l2n关于n的表达式.是 .
【答案】分析:(1)由变换T的定义“T将“0-1数列”A中原有的每个0都变成1,0”,直接可得数列A.
(2)设Ak中有bk个01数对,Ak+1中的00数对只能由Ak中的01数对得到,所以lk+1=bk,Ak+1中的01数对有两个产生途径:①由Ak中的1得到; ②由Ak中00得到,由此能求出l2n关于n的表达式.
解答:解:(1)∵数列A2:1,0,0,1,0,1,1,0,1,0,0,1,
∴由变换T的定义可得A1:0,1,1,0,0,1.…(2分)
A:1,0,1.…(4分)
(2)设Ak中有bk个01数对,Ak+1中的00数对只能由Ak中的01数对得到,
所以lk+1=bk,Ak+1中的01数对有两个产生途径:①由Ak中的1得到; ②由Ak中00得到,
由变换T的定义及A:0,1可得Ak中0和1的个数总相等,且共有2k+1个,
所以bk+1=lk+2k,
所以lk+2=lk+2k,
由A:0,1可得A1:1,0,0,1,A2:0,1,1,0,1,0,0,1,
所以l1=1,l2=1,
当k≥3时,
若k为偶数,lk=lk-2+2k-2,lk-2=lk-4+2k-4,…l4=l2+22.
上述各式相加可得lk=1+22+24+…+2k-2=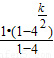 =
= (2k-1),
(2k-1),
经检验,k=2时,也满足lk= (2k-1).
(2k-1).
∴l2n= (4n-1).
(4n-1).
故答案为:1,0,1; (4n-1).
(4n-1).
点评:本题考查数列的应用,解题时要认真审题,注意新定义的准确理解,解题时要合理地挖掘题设中的隐含条件,恰当地进行等价转化.
(2)设Ak中有bk个01数对,Ak+1中的00数对只能由Ak中的01数对得到,所以lk+1=bk,Ak+1中的01数对有两个产生途径:①由Ak中的1得到; ②由Ak中00得到,由此能求出l2n关于n的表达式.
解答:解:(1)∵数列A2:1,0,0,1,0,1,1,0,1,0,0,1,
∴由变换T的定义可得A1:0,1,1,0,0,1.…(2分)
A:1,0,1.…(4分)
(2)设Ak中有bk个01数对,Ak+1中的00数对只能由Ak中的01数对得到,
所以lk+1=bk,Ak+1中的01数对有两个产生途径:①由Ak中的1得到; ②由Ak中00得到,
由变换T的定义及A:0,1可得Ak中0和1的个数总相等,且共有2k+1个,
所以bk+1=lk+2k,
所以lk+2=lk+2k,
由A:0,1可得A1:1,0,0,1,A2:0,1,1,0,1,0,0,1,
所以l1=1,l2=1,
当k≥3时,
若k为偶数,lk=lk-2+2k-2,lk-2=lk-4+2k-4,…l4=l2+22.
上述各式相加可得lk=1+22+24+…+2k-2=
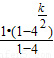 =
= (2k-1),
(2k-1),经检验,k=2时,也满足lk=
 (2k-1).
(2k-1).∴l2n=
 (4n-1).
(4n-1).故答案为:1,0,1;
 (4n-1).
(4n-1).点评:本题考查数列的应用,解题时要认真审题,注意新定义的准确理解,解题时要合理地挖掘题设中的隐含条件,恰当地进行等价转化.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目