题目内容
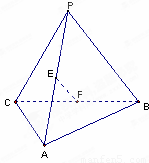
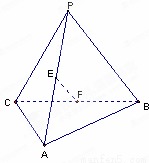
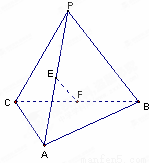
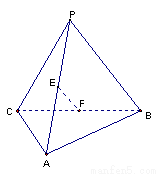
如图,E、F分别是三棱锥P-ABC的棱AP、BC的中点,PC=10,AB=6,EF=7,则异面直线AB与PC所成的角为( )
A.90° B.60° C.45° D.30°
【答案】
B
【解析】
试题分析:取AC中点G,连结EG,FG,FG是三角形ABC中位线,GF//AB,GF=AB/2=3,EG是三角形ACD中位线,EG//PC,EG=PC/2=5,故∠EGF是异面直线AB与PC所成角或所成角的补角。
在?EGF中,根据余弦定理,
cos∠EGF= 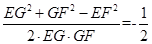 ,∠EGF=1200,异面直线AB与PC所成的角为600.
,∠EGF=1200,异面直线AB与PC所成的角为600.
考点:异面直线所成的角;余弦定理。
点评:本题主要考查了空间中异面直线所成的角。求异面直线所成角的步骤:一作二求三说。此题求出∠EGF=1200,但∠EGF并不是异面直线AB与PC所成角,而是所成角的补角。两异面直线所成角的范围为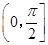 。
。

练习册系列答案
相关题目
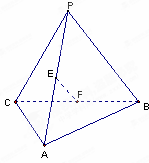 如图,E、F分别是三棱锥P-ABC的棱AP、BC的中点,PC=10,AB=6,EF=7,则异面直线AB与PC所成的角为( )
如图,E、F分别是三棱锥P-ABC的棱AP、BC的中点,PC=10,AB=6,EF=7,则异面直线AB与PC所成的角为( )| A、60° | B、45° | C、0° | D、120° |