题目内容
在极坐标系中,过点A(4,-| π | 2 |
分析:把极坐标转化为直角坐标,利用ρ2=x2+y2,ρsinθ=y,极坐标方程转化为直角坐标方程,如图:利用勾股定理求出切线长.
解答: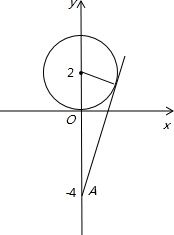 解:在极坐标系中,过点A(4,-
解:在极坐标系中,过点A(4,-
)引圆ρ=4sinθ的一条切线,
在直角坐标系下,A(0,-4),方程化为x2+y2-4y=0,
如图:圆心(0,2),半径:2
切线长为:
=4
故答案为:4
.
 解:在极坐标系中,过点A(4,-
解:在极坐标系中,过点A(4,-| π |
| 2 |
在直角坐标系下,A(0,-4),方程化为x2+y2-4y=0,
如图:圆心(0,2),半径:2
切线长为:
| 62-22 |
| 2 |
故答案为:4
| 2 |
点评:本题考查点的极坐标和直角坐标的互化,考查转化思想,计算能力,是基础题.

练习册系列答案
相关题目
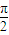 )引圆ρ=8sinθ的一条切线,则切线长为 .
)引圆ρ=8sinθ的一条切线,则切线长为 .