题目内容
平行四边形两条邻边的长分别为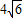 和
和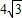 ,它们的夹角是45°,则它的面积为 .
,它们的夹角是45°,则它的面积为 .
【答案】分析:根据题意画出图形,如图,过A作AE垂直于BC,可得∠AEB为直角,在三角形ABE中,再由AB和B的度数,求出AE的长,然后由边BC与边上的高AE乘积即可求出平行四边形的面积.
解答: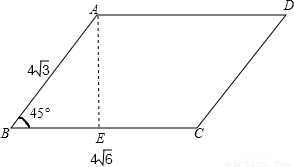 解:根据题意画出图形,如图所示:
解:根据题意画出图形,如图所示:
过A作AE⊥BC,则∠AEB=90°,又B=45°,AB=4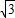 ,
,
得:AE=ABsin45°=2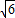 ,
,
则平行四边形的面积S=BC•AE=4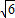 ×2
×2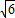 =48.
=48.
故答案为:48.
点评:此题考查了解直角三角形,以及特殊角的三角函数值,考查了数形结合的思想,熟练掌握正弦定理是解本题的关键.
解答:
 解:根据题意画出图形,如图所示:
解:根据题意画出图形,如图所示:过A作AE⊥BC,则∠AEB=90°,又B=45°,AB=4
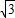 ,
,得:AE=ABsin45°=2
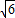 ,
,则平行四边形的面积S=BC•AE=4
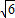 ×2
×2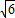 =48.
=48.故答案为:48.
点评:此题考查了解直角三角形,以及特殊角的三角函数值,考查了数形结合的思想,熟练掌握正弦定理是解本题的关键.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
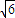 和
和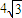 ,它们的夹角是
,它们的夹角是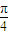 ,则平行四边形中较长的对角线的长是 .
,则平行四边形中较长的对角线的长是 .