��Ŀ����
����Ŀ��2020�괺���ڼ䣬��������״��������������ȫ����ɢ����ʡ�������ش�ͻ�����������¼�һ����Ӧ����ȡ��һϵ����Ч�ķ��ش�ʩ.��������¡���Ч�����.
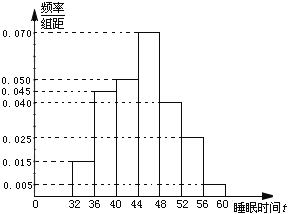
��1���ִ�������ij���������µǼDZ�������ɼ�100������.�ݷ�������Ⱥ���½��Ʒ�����̬�ֲ�![]() .��
.��![]() ��ʾ���ɼ�100����������ֵ��
��ʾ���ɼ�100����������ֵ��![]() ֮��ĵĸ�������
֮��ĵĸ�������![]() ��X����ѧ����.
��X����ѧ����.
��2�������ڼ䣬�人��ѧ����ҽԺ��֢��ң�ICU��������־���ŶӶ�138��ȷ�ﻼ�߽��и��ټ�¼.Ϊ�˷�������֢(complications)����֢����(ICU)�йصĿ��ų̶ȣ��ִӸ��Ŷӷ����ڹ��ʶ���ҽѧ�ڿ�JAMA������ҽѧ����־���о������л���������.�뽫����2��2�������������������ж��ܷ��ڷ�����ĸ��ʲ�����0.1%��ǰ������Ϊ����֢�����벢��֢�й�����

������![]() ����
����![]() ��
��![]() ��
��![]() ��
��![]() .
.
�ο���ʽ���ٽ�ֵ���� ������
������![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
���𰸡���1��![]() ��
��![]() ��2����������������ڷ�����ĸ��ʲ�����0.1%��ǰ������Ϊ����֢�����벢��֢�й���
��2����������������ڷ�����ĸ��ʲ�����0.1%��ǰ������Ϊ����֢�����벢��֢�й���
��������
(1)������̬�ֲ��Լ�����ֲ��ĸ��ʹ�ʽ����ѧ������ʽ�������.
(2)���ö����Լ���Ĺ�ʽֱ����⼴��.
��1������֪��������![]() ֮�ڵĸ���Ϊ
֮�ڵĸ���Ϊ![]() ��
��
������![]() ֮��ĸ���Ϊ
֮��ĸ���Ϊ![]() .
.
![]() .
.![]()
![]() ..
..
��2��������£�.
����֢ | ����֢ | �ϼ� | |
����֢ | 64 | 38 | 102 |
��֢ | 10 | 26 | 36 |
�ϼ� | 74 | 64 | 138 |
![]() .
.
��P(K210.828)=0.001��
���ɶ����Լ���������֪�����ڷ�����ĸ��ʲ�����0.1%��ǰ������Ϊ����֢�����벢��֢�й���.