题目内容
设函数
- A.
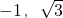
- B.
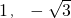
- C.
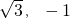
- D.
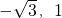
D
分析:利用辅助角公式可将f(x)=asinx-bcosx转化为f(x)= (sinx-φ),依题意可知
(sinx-φ),依题意可知 =2,φ=
=2,φ= +2kπ,k∈Z,从而可求得a,b的值.
+2kπ,k∈Z,从而可求得a,b的值.
解答:∵f(x)=asinx-bcosx转化为f(x)= sin(x-φ),(其中tanφ=
sin(x-φ),(其中tanφ= ),
),
∴由题意知, =2,
=2, -φ=2mπ-
-φ=2mπ- ,
,
∴φ= +2kπ,k∈Z,
+2kπ,k∈Z,
∴f(x)=2sin(x- )=2sinxcos(-
)=2sinxcos(- )+2cosxsin(-
)+2cosxsin(- )=-
)=- sinx-cosx,
sinx-cosx,
∴a=- ,b=1.
,b=1.
故选D.
点评:本题考查两角和与差的正弦函数,着重考查辅助角公式,求得 =2,φ=
=2,φ= +2kπ,k∈Z,是关键,也是难点,属于中档题.
+2kπ,k∈Z,是关键,也是难点,属于中档题.
分析:利用辅助角公式可将f(x)=asinx-bcosx转化为f(x)=
 (sinx-φ),依题意可知
(sinx-φ),依题意可知 =2,φ=
=2,φ= +2kπ,k∈Z,从而可求得a,b的值.
+2kπ,k∈Z,从而可求得a,b的值.解答:∵f(x)=asinx-bcosx转化为f(x)=
 sin(x-φ),(其中tanφ=
sin(x-φ),(其中tanφ= ),
),∴由题意知,
 =2,
=2, -φ=2mπ-
-φ=2mπ- ,
,∴φ=
 +2kπ,k∈Z,
+2kπ,k∈Z,∴f(x)=2sin(x-
 )=2sinxcos(-
)=2sinxcos(- )+2cosxsin(-
)+2cosxsin(- )=-
)=- sinx-cosx,
sinx-cosx,∴a=-
 ,b=1.
,b=1.故选D.
点评:本题考查两角和与差的正弦函数,着重考查辅助角公式,求得
 =2,φ=
=2,φ= +2kπ,k∈Z,是关键,也是难点,属于中档题.
+2kπ,k∈Z,是关键,也是难点,属于中档题. 
练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
 ,图像的最高点从左到右依次记为
,图像的最高点从左到右依次记为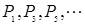 ,函数
,函数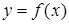 的图像与
的图像与 轴的交点从左到右依次记为
轴的交点从左到右依次记为 ,设
,设 则
则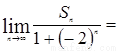 ( )
( )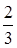 B.
B.
 C.
C.
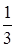 D.
D.

 个单位,得到一个偶函数的图象
个单位,得到一个偶函数的图象 ]上为增函数
]上为增函数 ,图像的最高点从左到右依次记为
,图像的最高点从左到右依次记为 ( )
( )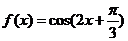 ,则下列结论中正确的是( )
,则下列结论中正确的是( )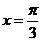 对称 ②f(x)的图像关于点
对称 ②f(x)的图像关于点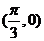 对称
对称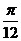 个单位,得到一个偶函数的图像 ④f(x)在
个单位,得到一个偶函数的图像 ④f(x)在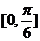 上为减函数
上为减函数