题目内容
给出两条直线l1和l2，斜率存在且不为0，如果满足斜率互为相反数，且在y轴上的截距相等，那么直线l1和l2叫做“孪生直线”.(1)现在给出4条直线的参数方程如下:
l1:
(t为参数);
l2: 
(t为参数);
l3:
(t为参数);
l4:
(t为参数).
其中构成“孪生直线”的是____________.
(2)给出由参数方程表示的直线l1: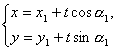
(t为参数),
直线l2:
(t为参数),
那么，根据定义，直线l1,直线l2构成“孪生直线”的条件是__________________.
解析:根据条件,两条直线构成“孪生直线”意味着它的斜率存在不为0,互为相反数,且在y轴的截距相等,也就是在y轴上交于同一点.
对于题(1),首先可以判断出其斜率分别为-1,1,-1,1,斜率互为相反数条件很明显,再判断在y轴上的截距.
令x=0得出相应的t值,代入y可得只有直线l1和直线l4在y轴上的截距相等,而其斜率又恰好相反,可以构成“孪生直线”.
对于题(2)首先写出相应斜率分别是tanα1和tanα2,
因此要tanα1=-tanα2,即tanα1+tanα2=0；
然后再考虑在y轴上的截距,首先在l1的参数方程中,令x=x1+tcosα1=0,
可得t=代入得y=y1-x1tanα1.
同理,可得直线l2在y轴上的截距是y=y2-x2tanα2.
由定义中的条件“截距相等”可得y1-x1tanα1=y2-x2tanα2,
即y1-y2=x1tanα1-x2tanα2.
如果把tanα1=-tanα2代入式子还可以进一步得到y1-y2=x1tanα1+x2tanα1,即y1-y2=(x1+x2)tanα1.
答案:（1）直线l1和直线l4
（2）tanα1+tanα2=0且y1-y2=x1tanα1+x2tanα2〔也可以写成y1-y2=(x1+x2)tanα1〕.
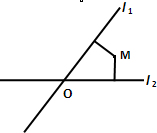
如图，平面中两条直线l1和l 2相交于点O，对于平面上任意一点M，若x，y分别是M到直线l 1和l 2的距离，则称有序非负实数对（x，y）是点M的“距离坐标”．已知常数p≥0，q≥0，给出下列三个命题：
