题目内容
将函数
的图像沿
轴向右平移
个单位
，所得图像关于
轴对称，则的最小值为
A． | B． | C． | D． |
C
解析试题分析：∵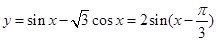
，∴沿x轴向右平移a个单位得到
，由它的图象关于y轴对称知2sin（x-a-）=2sin（-x-a-），
∴sinxcos（a+）=0，∴cos（a+）=0，∴a+=+kπ，∴α=+kπ，∴a的最小值为，故选C
考点：本题考查了两角和与差的正弦公式、平移的左加右减的原则、和三角函数的奇偶性．
点评：熟练运用两角和与差的公式是解决此类问题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知函数
上有两个零点，则m的取值范围是
| A．（1,2） | B．[1,2） | C．（1,2] | D．[l,2] |
已知角
的终边上一点的坐标为（
,
），则角的最小正值为（ ）
A． | B． | C． | D． |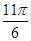
已知
为偶函数，则
可以取的一个值为（ ）
A． | B． | C．－ | D．－ |
若
，则
的值是（ ）
A． | B． | C． | D． |
要得到函数
的图像，可以把函数
的图像（ ）
A．向右平移 个单位 | B．向左平移个单位 |
C．向右平移 个单位 | D．向左平移个单位 |
函数
的单调递增区间是（ ）
A． | B． |
C． | D． |
已知函数
其中（
）则“
”是“
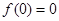是奇函数”的( )
| A．充分但不必要条件 | B．必要但不充分条件 |
| C．充要条件 | D．既非充分也非必要条件 |
函数
是
上的偶函数，则
的值是 ( ）
A． | B． | C． | D． |