题目内容
已知函数f(x)=x2+(a+2)x+b满足f(-1)=-2;
(1)若方程f(x)=2x有唯一的解;求实数a,b的值;
(2)若函数f(x)在区间[-2,2]上不是单调函数,求实数a的取值范围。
解:(1)由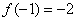 知,b-a+1=0,①
知,b-a+1=0,①
又f(x)=2x有唯一的解,故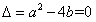 ,
,
将①式代入上式得: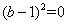 ,故b=1,
,故b=1,
代入①得,a=2。
(2)因为函数f(x)在区间[-2,2]上不是单调函数,
所以,对称轴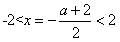 ,解得:
,解得: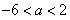 ,
,
∴a的取值范围是(-6,2)。
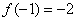 知,b-a+1=0,①
知,b-a+1=0,①又f(x)=2x有唯一的解,故
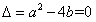 ,
,将①式代入上式得:
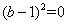 ,故b=1,
,故b=1,代入①得,a=2。
(2)因为函数f(x)在区间[-2,2]上不是单调函数,
所以,对称轴
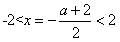 ,解得:
,解得: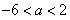 ,
,∴a的取值范围是(-6,2)。

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目