题目内容
(本题满分14分)
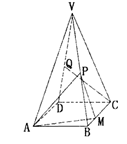
如图,已知平面QBC与直线PA均垂直于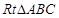 所在平面,且PA=AB=AC.
所在平面,且PA=AB=AC.

(Ⅰ)求证:PA∥平面QBC;
(Ⅱ)若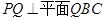 ,求二面角Q-PB-A的余弦值。
,求二面角Q-PB-A的余弦值。
如图,已知平面QBC与直线PA均垂直于
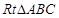 所在平面,且PA=AB=AC.
所在平面,且PA=AB=AC.
(Ⅰ)求证:PA∥平面QBC;
(Ⅱ)若
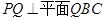 ,求二面角Q-PB-A的余弦值。
,求二面角Q-PB-A的余弦值。(1)通过已知中的平面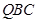 ⊥平面
⊥平面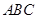 ,那么结合
,那么结合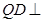 平面
平面 ,和
,和 ⊥平面
⊥平面 ,从而得到线线平行
,从而得到线线平行 ∥
∥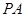 ,利用线面平行的性质来证明。
,利用线面平行的性质来证明。
(2)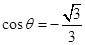
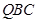 ⊥平面
⊥平面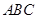 ,那么结合
,那么结合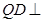 平面
平面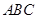 ,和
,和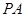 ⊥平面
⊥平面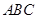 ,从而得到线线平行
,从而得到线线平行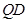 ∥
∥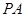 ,利用线面平行的性质来证明。
,利用线面平行的性质来证明。(2)
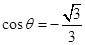
试题分析:解:(I)证明:过点
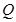 作
作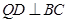 于点
于点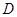 ,
,
∵平面
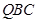 ⊥平面
⊥平面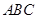 ∴
∴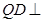 平面
平面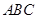
又∵
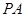 ⊥平面
⊥平面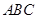
∴
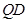 ∥
∥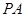 又∵
又∵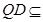 平面
平面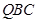
∴
 ∥平面
∥平面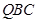 ……6分
……6分(Ⅱ)∵
 平面
平面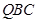
∴
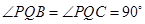 又∵
又∵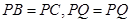
∴
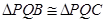 ∴
∴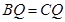
∴点
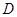 是
是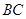 的中点,连结
的中点,连结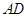 ,则
,则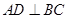
∴
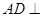 平面
平面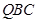 ∴
∴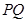 ∥
∥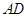 ,
,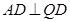
∴四边形
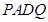 是矩形 ……8分
是矩形 ……8分设
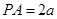
∴
 ,
,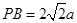 ∴
∴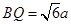
过
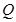 作
作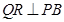 于点
于点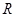 ,
,∴
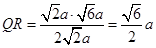 ,
,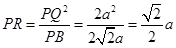
取
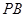 中点
中点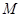 ,连结
,连结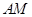 ,取
,取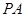 的中点
的中点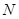 ,连结
,连结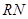
∵
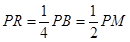 ,
,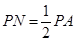 ∴
∴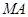 ∥
∥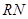
∵
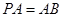 ∴
∴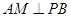 ∴
∴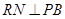
∴
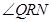 为二面角
为二面角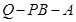 的平面角……12分
的平面角……12分连结
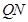 ,则
,则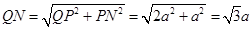 又∵
又∵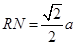
∴
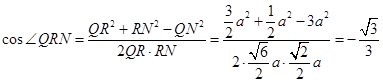
即二面角
 的余弦值为
的余弦值为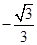 ……14分
……14分方法二:
(I)同方法一 ……………………………………6分
(Ⅱ)∵
 平面
平面
∴
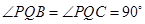 ,又∵
,又∵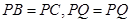
∴
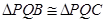 ∴
∴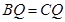
∴点
 是
是 的中点,连结
的中点,连结 ,则
,则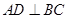
∴
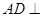 平面
平面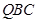 ∴
∴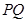 ∥
∥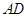 ,
,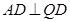
∴四边形
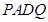 是矩形 ……………………8分
是矩形 ……………………8分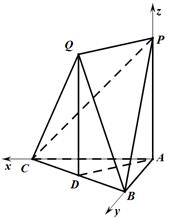
分别以
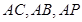 为
为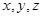 轴建立空间直角坐标系
轴建立空间直角坐标系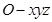
设
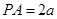 ,则
,则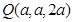 ,
,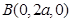 ,
,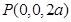 ,
,设平面
 的法向量为
的法向量为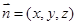
∵
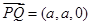 ,
,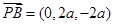
∴
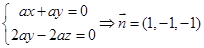
又∵平面
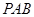 的法向量为
的法向量为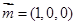 ……12分
……12分设二面角
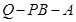 为
为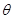 ,则
,则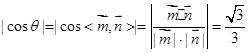
又∵二面角
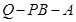 是钝角
是钝角∴
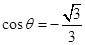 ………………………………14分
………………………………14分点评:解决该试题的关键是利用线面平行的判定定理分析得到第一问,这是一般的解题思路,同时对于二面角的求解可以先作,后证明,再解,也可以建立直角坐标系,进而结合向量的知识来分析得到结论,属于中档题。

练习册系列答案
相关题目
 中,平面
中,平面 平面
平面 ,
,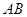 ∥
∥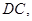
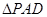 是正三角形,已知
是正三角形,已知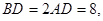
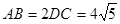
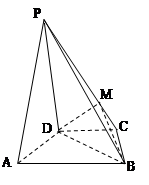
 是
是 上的一点,求证:平面
上的一点,求证:平面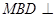 平面
平面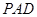 ;
; 和平面
和平面 ,下列四个命题中,正确的是( )
,下列四个命题中,正确的是( ) 则
则


 则
则


 一边BC在平面
一边BC在平面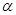 内,顶点A在平面
内,顶点A在平面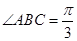 ,三角形所在平面与
,三角形所在平面与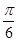 ,则直线
,则直线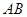 与
与
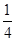
 是两不同直线,
是两不同直线,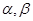 是两不同平面,则下列命题错误的是
是两不同平面,则下列命题错误的是 ,
, ∥
∥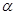 ,则
,则
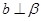 ,
,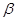 ,则
,则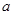 ∥
∥ ,则
,则
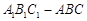 中,侧面
中,侧面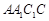
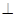 底面ABC,侧面
底面ABC,侧面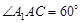 ,E、F分别是
,E、F分别是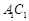 、AB的中点.
、AB的中点.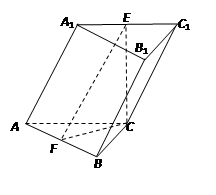
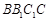 ;
;
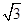 ,VA =" 6."
,VA =" 6."