Question

一个圆环直径为2

2

m，通过铁丝BC，CA₁，CA₂，CA₃（A₁，A₂，A₃是圆上三等分点）悬挂在B处，圆环呈水平状态并距天花板2m，如图所示．设BC长为x（m），问当x取多长时，铁丝总长y有最小值，并求此最小值．

Answer 1

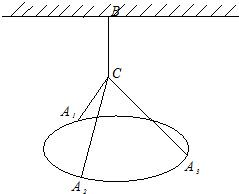
分析：根据题意C，A₁，A₂，A₃四点构成一个正三棱锥，然后利用侧棱的长度求导，判断单调区间，最后根据函数单调性求最值．

解答：解：由题意C，A₁，A₂，A₃四点构成一个正三棱锥，
CA₁，CA₂，CA₃为该三棱锥的三条侧棱．
三棱锥的侧棱CA1=

(2-x)2+2

；
于是有y=x+3

(2-x)2+2

．（0＜x＜2）
对y求导得y′=1-

3(2-x)

(2-x)2+2

．
令y'=0得9（2-x）²=（2-x）²+2，
解得x=

3

2

或x=

5

2

（舍）．
当x∈(0，

3

2

)时，y'＜0，
当x∈(

3

2

，2)时，y'＞0．
故当x=

3

2

时，即BC=1.5m时，y取得最小值为6m．

点评：本题考查函数模型的选择与应用，通过对实际问题的分析，抽象出数学模型，利用导数判断单调性并求解，属于基础题．